Darcy – Weisbach Pressure Drop Per Mile

Introduction

Darcy-Weisbach equations are valid for steady state flow. The friction factor – λ -depends on the flow, (laminar, transient, turbulent, Reynolds number) and the internal roughness of the pipe. The friction coefficient can be calculated by the Colebrook-White equation.

Limitations of this calculation depend on the flow regime for the right friction factor or coefficient. Many factors affect the head loss in pipes, the viscosity of the fluid being handled, the size of the pipes, the roughness of the internal surface of the pipes, the changes in elevations within the system and the length of travel of the fluid. : H_L=f\bigg( \frac{L}{D}\bigg)\frac{v^2}{2g}

H_L=f\bigg( \frac{L}{D}\bigg)\frac{v^2}{2g}

𝐻_𝐿 − Head Loss [ft]

f – Friction Factor

𝐿 − Pipe Length [ft]

𝐷 − Internal Pipe Diameter [in]

𝑣 − Flowing Velocity [ft/sec]

𝑔 − Gravitational Constant [ft²/sec]

Friction factor is solved using Newton-Raphson method

f=\frac{64}{Re};\,Laminar\,Flow: Re < 2000 \~\ \frac{1}{\sqrt{f}}=2\log_{10}(Re\sqrt{f})-0.8;\,Smooth\,Pipe:Re >4000\,and\,\frac{\varepsilon}{D}\rightarrow0\~\ \frac{1}{\sqrt{f}}=-2\log_{10}\biggr(\frac{\varepsilon}{3.7D}+\frac{2.51}{Re\sqrt{f}}\biggr);\,Transitional,\,Colebrook-White\,Eq,Re>4000\~\ \frac{1}{\sqrt{f}}=1.14-2\log_{10}\biggr(\frac{\varepsilon}{D}\biggr);\,Wholly \,Rough

f=\frac{64}{Re};\,Laminar\,Flow: Re < 2000 \\~\\ \frac{1}{\sqrt{f}}=2\log_{10}(Re\sqrt{f})-0.8;\,Smooth\,Pipe:Re >4000\,and\,\frac{\varepsilon}{D}\rightarrow0\\~\\ \frac{1}{\sqrt{f}}=-2\log_{10}\biggr(\frac{\varepsilon}{3.7D}+\frac{2.51}{Re\sqrt{f}}\biggr);\,Transitional,\,Colebrook-White\,Eq,Re>4000\\~\\ \frac{1}{\sqrt{f}}=1.14-2\log_{10}\biggr(\frac{\varepsilon}{D}\biggr);\,Wholly \,Rough

𝑓 − Friction Factor

D – Inside Pipe Diameter[in]

𝜀 − Pipe Roughness[in]

\Delta\rho=\lambda\bigg(\frac{L}{D_h}\bigg)\bigg(\frac{\rho v^2}{2}\bigg)

\Delta\rho=\lambda\bigg(\frac{L}{D_h}\bigg)\bigg(\frac{\rho v^2}{2}\bigg)

Where:

∆𝜌 − Pressure Loss [psi/mile]

𝜆 – Darcy-Weisbach Fiction Coefficient

𝐿 − Pipe Length [ft]

𝐷_ℎ − Hydraulic Diameter [in]

𝑣 − Velocity [ft/sec]

𝜌 − density [lb/ft²]

Case Guide

Part 1: Create Case

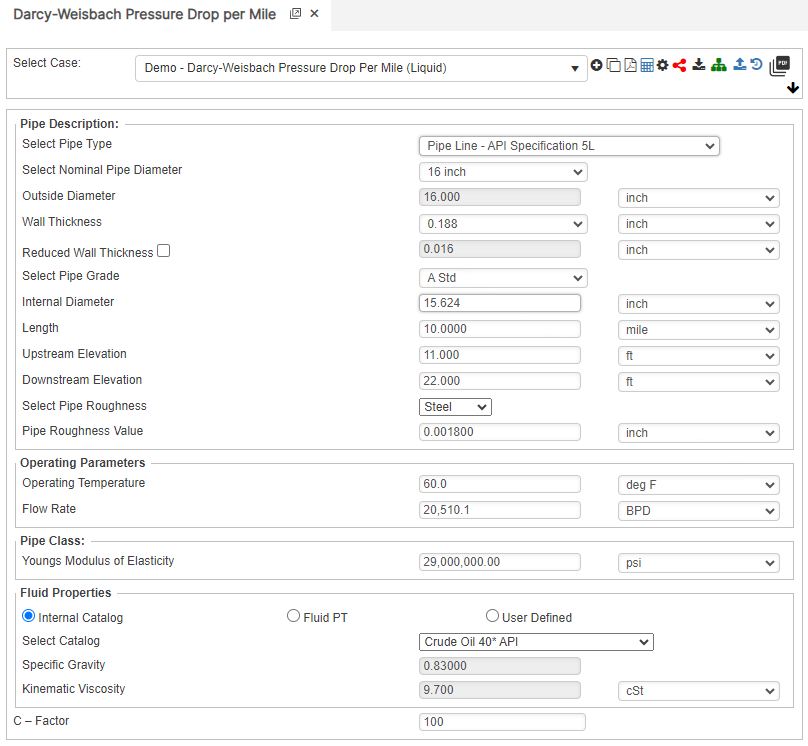
Input Parameters

• Pipe Type
• Pipe Outside Diameter
• Pipe Wall Thickness
• Flowing Temperature (°F)
• Absolute Pipe Roughness
• Specific Gravity
• Flow Rate(Barrels per Day)
• Internal Pipe Diameter(in)
• Kinematic Viscosity
• Length of Pipeline(mi)
• Upstream Elevation(ft)
• Downstream Elevation(ft)

Pressure Drop per Mile

Part 2: Outputs/Reports

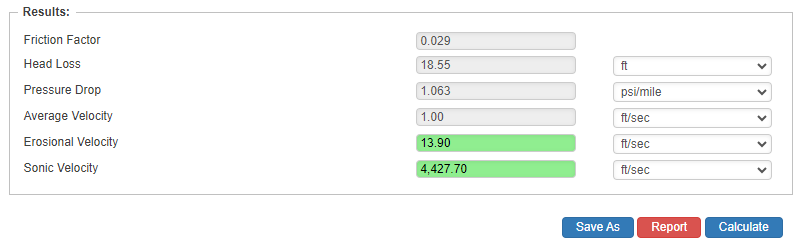
Results

• Friction Factor
• Heal Loss (ft)
• Pressure Drop (psi/mi)
• Average Velocity (ft/sec)
• Erosional Velocity (ft/sec.)
• Sonic Velocity (ft/sec.)

Pressure Drop per Mile

References

• “Pipeline Rules of Thumb” Gulf Professional Publishing, Seventh Edition, McAllister, E. W.
• “Gas Pipeline Hydraulics”, Systek Technologies, Inc., Menon, Shahi E.
• “Advanced Pipeline Design”, Carroll, Landon and Hudkins, Weston R.
• American Gas Association (AGA), “Reference: Eq-17-18, Section 17, GPSA”, Engineering Data Book, Eleventh Edition
• Hydraulic Transients, McGraw-Hill, New York., Streeter, V.L. and Wylie, E.B. (1967)
• Water Hammer Analysis. Jour. Hyd. Div., ASCE., Vol. 88, HY3, pp79-113 May, Streeter, V.L. (1969)
• Unsteady flow calculations by numerical methods’, Jour. Basic Eng., ASME., 94, pp457-466, June. Streeter, V.L. (1972),
• Hydraulic Pipelines, John Wiley & Sons, J. P Tullis (1989)

FAQ