Absolute Stability Method Analysis

Introduction

In the ASM analysis, the pipeline is checked for absolute lateral stability based on DNV-RP-F109, On- Bottom Stability Design of Submarine Pipelines [2].

Absolute static requirement for lateral on-bottom stability is based on a static equilibrium of forces that ensures that the resistance of the pipe against motion is sufficient to withstand maximum hydrodynamic loads during a sea state, i.e. the pipe will experience no lateral displacement under the design extreme conditions in the sea state considered.

“Extreme horizontal” and “extreme vertical” forces are applied together on pipeline, whereas the phase angles of drag, lift and inertia forces are ignored in this calculation.

Furthermore, this criterion of zero displacement often leads to the requirement for heavy pipes. This is because, with zero displacement, one cannot take advantage of the increased passive resistance built up due to the penetration caused by the pipe being rugged back and forth by the wave induced flow.

The following two criteria are to be met to satisfy the absolute lateral static stability requirement:

\gamma_{sc} \cdot \frac{F_Y^* + \mu \cdot F_Z^}{\mu\cdot \text{w}s + F_R} \leq 1.0\~\ \text{and}\~\ \gamma{sc} \cdot\frac{F_Z^}{\text{w}_s} \leq 1.0

\gamma_{sc} \cdot  \frac{F_Y^* + \mu \cdot  F_Z^*}{\mu\cdot  \text{w}_s + F_R} \leq 1.0\\~\\ \text{and}\\~\\ \gamma_{sc} \cdot\frac{F_Z^*}{\text{w}_s} \leq 1.0

Where:

• F_Y^* is the peak horizontal load
• F_Z^* is the peak vertical load
• γ_SC is the safety factor for absolute lateral stability
• F_R is the soil passive resistance
• μ is the coefficient of friction between the pipe outer surface and the soil
• w_s is the submerged weight of pipe

The following assumptions are applicable:

• The spectral wave is calculated based on a 3-hour storm.
• The calculation methodology considers monotonic loading only; the cyclical movements of the pipe are not taken into account.
• The friction coefficient is based on the values for concrete coated pipe as given in DNV-RP-F109 [2].
• For non-permeable seabed, the load reduction due to seabed penetration is taken as equal to 1.0 (i.e. no load reduction).
• When the vertical contact force between the pipe and soil is less than or equal to zero, the passive soil resistance is taken as zero.
• No piggy backed lines are considered in the calculations.
• No reduction due to piping of sand layers is taken into account.
• Soil properties are taken as constant with depth.

ASM Input Data Tab

The Input Data tab allows the user to enter all the required parameter values for calculation, as presented in Figure 6-1.

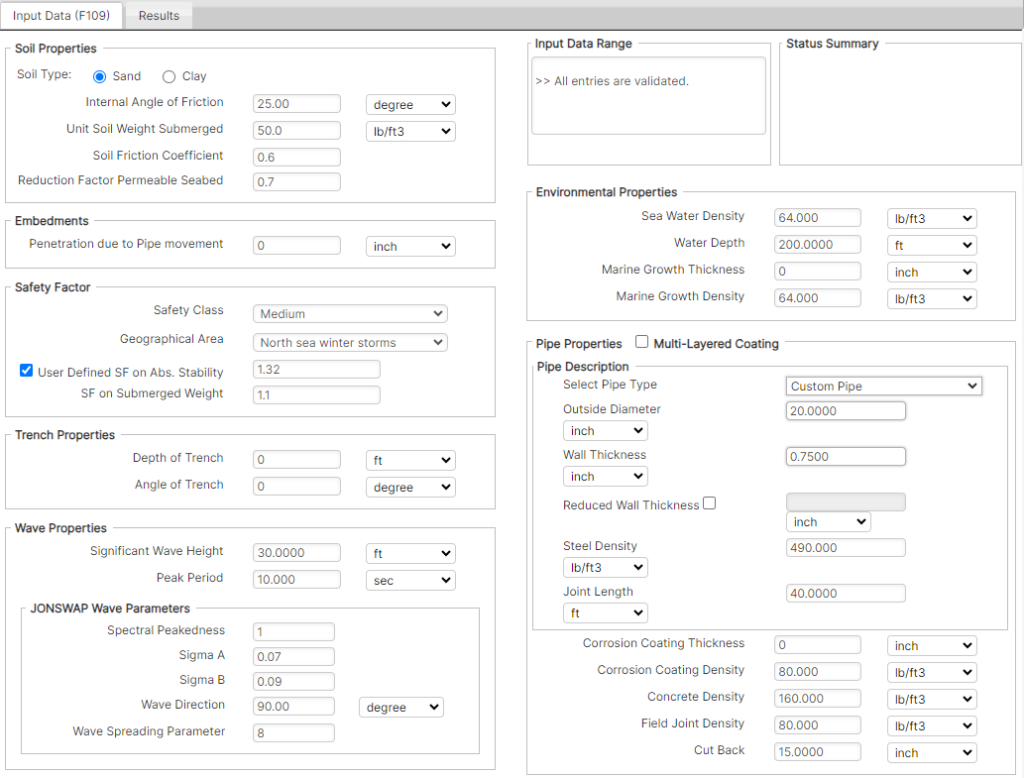
Pipe Properties

Outer Diameter -The outer diameter of the steel pipe.
Wall Thickness – The wall thickness of the steel pipe.
Corrosion Coating Thickness – Thickness of the external corrosion (or insulation) coating.
Corrosion Coating Density – Density of the external corrosion (or insulation) coating.
Concrete Density – Density of the external concrete weight coating.
Field Joint Density – Density of the field joint coating and infill.
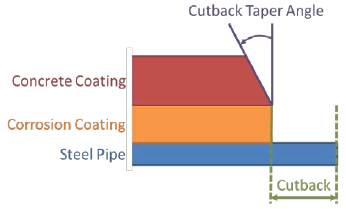
Cutback – Cutback in the concrete coating at each end of the pipe joint, as presented in Figure 3-2. The ASM calculations assume a taper angle of 0° from the radial direction of the pipe.
Cutback Taper Angle – Taper angle of concrete coating, referenced from the radial direction, as presented in Figure 3-2.
Product Density – Density of the product/contents inside the pipeline.
Joint Length – The nominal length of one pipe joint.
Steel Density – Density of the steel pipe.

Multi-Layered Coating – If this option is checked, an additional set of input fields appear on the input form under the heading of Multi-Layered Coating, as shown in Figure 4-7. The thickness and density of up to four coating layers can be specified to compute the equivalent coating thickness and density. When using the multi-layered coating option, the standard inputs for the thickness and density of the corrosion coating are disabled, with the calculations using the computed equivalent values instead.

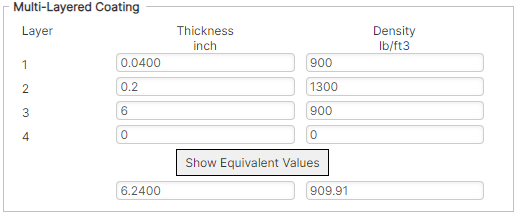
The multi-layered coating section includes the following:

• Layer: numerical index of the coating layer, numbered ascendingly from innermost to outermost layer.
• Thickness: the thickness of each corresponding coating layer.
• Density: the density of each corresponding coating layer.
• Show Equivalent Values: pressing this button calculates and displays the equivalent thickness and density for the coatings specified in the Multi-Layered Coating fields.

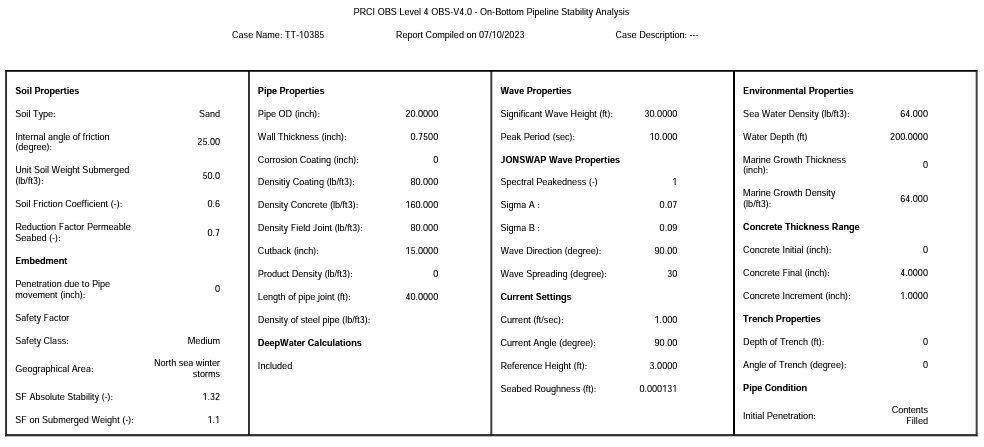
Soil Properties

Soil Type – The type of soil is selectable from two options listed under this heading and covered by DNV-RP-F109 [2], which are defined by different parameters:

• Sand
  • Internal angle of friction
  • Unit submerged weight of sand soil
• Clay
  • Undrained shear strength
  • Dry unit weight of clay soil

Soil Friction Coefficient – The value of friction coefficient between the soil and the external surface of the pipe. DNV-RP-F109 [2] suggests a value of 0.2 for a concrete-coated pipe on clay and 0.6 for a concrete-coated pipe on sand.
Reduction Factor Permeable Seabed – The permeable seabed reduction factor can be applied to take consideration of flow in the seabed underneath the pipe, reducing the vertical load. DNV-RP-F109 [2] suggests a reduction factor value of 0.7 for a permeable seabed, such as sand.

Embedment

Penetration due to Pipe Movement – Pipe penetration due to pipe movement can be entered in this field. This value can typically be obtained from installation analysis.

Safety Factors

Safety Class – Safety class level for the pipeline in accordance with DNV-OS-F101 [4], selectable from the options of Low, Medium and High

The safety classes are broadly defined such that a failure under each corresponds to:

• Low: insignificant risk of human injury and minor environmental and economic consequences.
• Medium: low risk of human injury, minor environmental pollution or high economic or political consequences.
• High: risk of human injury, significant environmental pollution or very high economic or political consequences.

Geographical Area – This refers to the geographical location of the laid pipeline. The selection of this value, the soil type, and the safety class results in the determination of an applicable absolute stability safety factor to use in the analysis, in accordance with DNV-RP-F109 [2].
User Defined Safety Factor – This field allows the overwriting of the code absolute stability safety factor, as described in Geographical Area, with a user defined value. This may be applicable if the laid pipeline is located in a different area from the DNV-RP-F109 [2] geographical locations available in the list or if more project-relevant safety factor information is available.
Safety Factor on Submerged Weight – This numerical value (γw in the equation below) defines the safety factor to be applied to the vertical stability check (as distinct from the absolute stability check), which assesses the potential of flotation of the pipe:

\gamma_{w} \cdot\frac{b}{\text{w}_s+b} \leq 1.0

\gamma_{w} \cdot\frac{b}{\text{w}_s+b} \leq 1.0

Trench Properties

Depth of Trench – This defines the depth of any trench the pipe sits in (z_t in Figure 6-2), referenced from the bottom of the trench to the general seabed level at a width not greater than three pipe diameters away from the pipe, as presented in Figure 6-2.

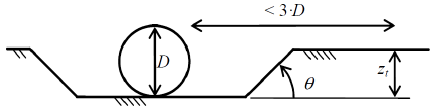
Angle of Trench – This defines the angle of the pipe trench with respect to the horizontal, as presented in Figure 6-2 as θ.

Environmental Properties

Seawater Density – Density of the seawater at the pipe location.
Water Depth – Depth of the sea from free surface to the seabed at the pipe location.
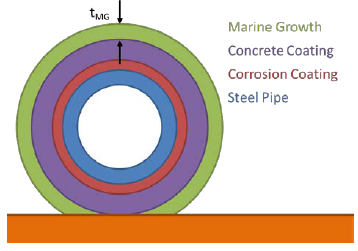
Marine Growth Density – Density of the marine growth on the external surface of the pipe.
Marine Growth Thickness (ASM) – Thickness of the marine growth, taken as a full circumferential layer on the outermost surface of the pipe, illustrated in Figure 6-3 without embedment, as denoted t_MG.

Wave Properties

Surface Wave Spectra – The wave is defined by the surface wave parameters, which are used to calculate the wave loads near the seabed:

• Significant Wave Height: the vertical distance from trough to crest of the significant wave.
• Peak Period: the time interval between successive peak wave crests passing a particular point.

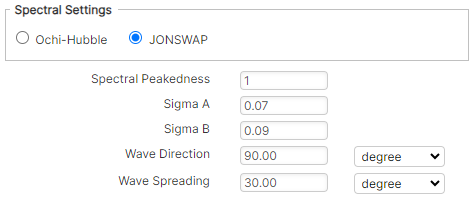
JONSWAP – This single peak spectrum was initially formulated as a modification of the Pierson-Moskowitz spectrum to describe a developing sea state in a fetch limited situation. It is often applied to on-bottom stability analyses, and is defined by the following parameters, as presented in Figure 4-12.

• Spectral Peakedness: The dimensionless peakedness parameter for the JONSWAP spectrum.
• Sigma A: JONSWAP spectral width parameter, applicable when 𝜔≤𝜔_𝑝.
  Where:
  • ω is the wave angular frequency
  • ω_p is the wave angular spectral peak frequency
• Sigma B: JONSWAP spectral width parameter, applicable when 𝜔>𝜔_𝑝.
• Wave Direction: the angle of wave propagation relative to the pipeline (perpendicular to the pipe is 90°).
• Wave Spreading: the standard deviation of wave spreading used in the wrapped normal spreading function.

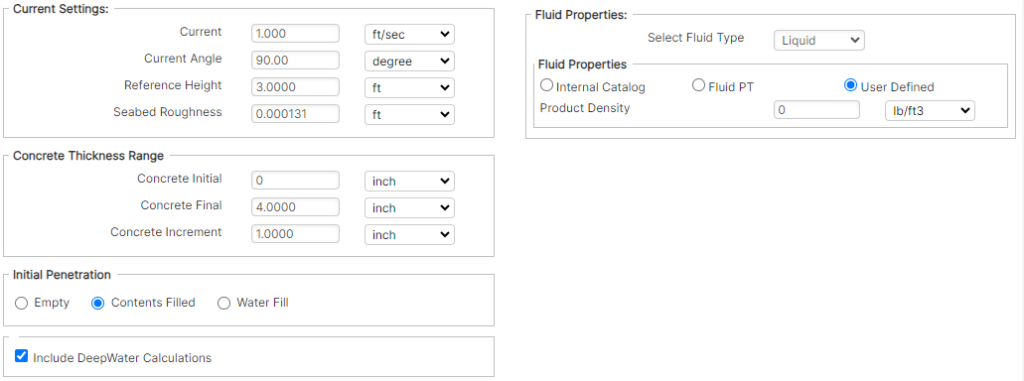
Current Settings

The values describing the steady current are input in this area.
The type of boundary layer calculation applied by the software in the ASM analysis is that given in DNV-RP-F109 [2]; described as:

V(z) = V(z_r) \cdot \frac{\ln(z + z_0) – \ln(z_0)}{\ln(z_r + z_0) – \ln(z_0)} \cdot \sin(\theta_c)

V(z) = V(z_r) \cdot \frac{\ln(z + z_0) - \ln(z_0)}{\ln(z_r + z_0) - \ln(z_0)} \cdot \sin(\theta_c)

Where:

• V(z) is the current speed at elevation above seabed z
• z_r is the current reference height
• z₀ is the seabed roughness
• θ_c is the angle of the current, with respect to the pipeline

Current – The speed of the current, which acts at the reference height in the direction specified by the current angle.
Current Angle – The angle of attack at which the current acts on pipeline (perpendicular to the pipe is 90°).
Reference Height – The height above the seabed at which the current value is known (taken as the top of the boundary layer).
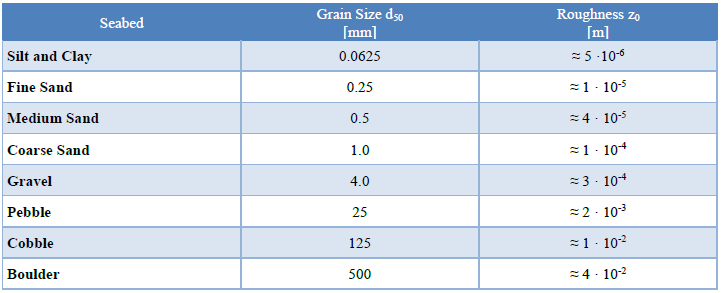
Seabed Roughness – Based on the seabed type Seabed roughness value can be input in this field. Reference can made from Table 3-1, as given in DNV-RP-F109 [2].

Concrete Thickness Range

Concrete Initial – The starting value of concrete thickness for the parameter incrementing, which represents its minimum value.
Concrete Final – The final value of concrete thickness for the parameter incrementing, which represents its maximum value.
Concrete Increment – The value at which the concrete thickness is incremented, from Initial value to Final value. The incremented values appear as separate entries in the outputs.

Include Deepwater Calculations

Checking this option will consider the horizontal peak load formula as given below and described in the DNV On-Bottom Stability in Deep Waters note [5]. This modified load formula accounts for calculation behavior that can occur for deepwater scenarios when the Keulegan-Carpenter number is low and the hydrodynamics are dominated by steady current.

This option may typically be selected when the on-bottom stability check is performed for a pipeline laid in deep waters (where current action is more than wave action). The option may be unselected for a shallow water analysis (where wave action is more than current action), however this is not required, as for non-small KC numbers, the modified load formula matches the DNV-RP-F109 [2] formulation.

K^* \geq 2.5: F_Y^* = r_{tot,y}\cdot\frac{1}{2}\cdot \rho_w \cdot D \cdot C_Y^* \cdot (U^* + V^)^2 \~\ K^ \leq 2.5: F_Y^* = r_{tot,y}\cdot\frac{1}{2}\cdot \rho_w \cdot D \cdot \left(C_Y^* \cdot (U^* + V^)^2 + \frac{C_M^ \cdot \pi^2}{K^} \cdot U^{2}\right), \~\ C_Y^* = 1.00, \quad C_M = 3.29

K^* \geq 2.5: F_Y^* = r_{tot,y}\cdot\frac{1}{2}\cdot \rho_w \cdot D \cdot C_Y^* \cdot (U^* + V^*)^2 \\~\\ K^* \leq 2.5: F_Y^* = r_{tot,y}\cdot\frac{1}{2}\cdot \rho_w \cdot D \cdot \left(C_Y^* \cdot (U^* + V^*)^2 + \frac{C_M^* \cdot \pi^2}{K^*} \cdot U^{*2}\right), \\~\\ C_Y^* = 1.00, \quad C_M = 3.29

Initial Penetration

This area presents three condition options for the consideration of the pipe self-weight to use to determine the initial penetration: Empty, Contents Filled and Water Filled. The software will automatically calculate the initial pipe penetration value for the chosen pipe condition in accordance with DNV-RP-F109 [2].

The condition of the pipe in its initial configuration at the beginning of the stability analysis should be considered, and not necessarily the contents of the analyzed condition itself. For example, if analyzing the stability of a pipeline in operation, although the contents during operation would correspond to Contents Filled, for an operating condition subsequent to hydrotest of the line, it may be more appropriate to select Water Filled, given that the maximum embedment will have already been achieved for the pipe full of water, prior to operation.

However, the consideration of an Empty pipe may also be a valid choice for the same scenario, if it is desired to reduce the beneficial effects of initial embedment for the stability analysis.

ASM Output Data Tab

The output can be viewed by clicking the Output Data tab, which displays the results outlined in this section in the chosen unit system, as presented in Figure 6-4. The outputs are also exported in PDF format. The PDF file can be opened by clicking on the Report button option in the ribbon menu.

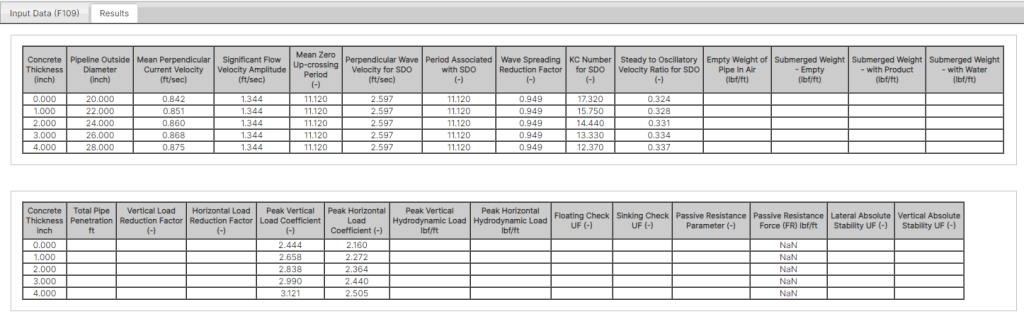
Hydrodynamic Outputs

Wave Length – The wave length is calculated based on the input wave properties, and describes the distance between successive wave crests.
Keulegan-Carpenter (without Concrete) – The Keulegan-Carpenter (KC) number calculated without considering a concrete coating on the pipe, which describes the relative importance in oscillatory flow of the drag forces over the inertia forces. The general form for the KC number is given by:

KC = \frac{U_{oscillatory} \cdot T}{D}

KC = \frac{U_{oscillatory} \cdot T}{D}

Where:

• U_oscillatory – The oscillatory velocity
• T – The period
• D – The outermost diameter under consideration (which excludes the concrete coating in this output column)

Current Ratio – The ratio of steady current to oscillatory current, considering the mean current over one pipe diameter:

\alpha = \frac{U_{steady}}{U_{oscillatory}}

\alpha = \frac{U_{steady}}{U_{oscillatory}}

Wave Induced Bottom Particle Velocity Normal to the Pipe – This field displays the wave bottom velocity perpendicular to the pipe; calculated using Airy wave theory.
Wave Induced Bottom Particle Acceleration Normal to the Pipe – This field displays the wave induced bottom acceleration perpendicular to the pipe; calculated using Airy wave theory.

General

Concrete Thickness – Displays the range of concrete thickness in the increments defined in the Input Data tab, with the first and last values in this column being the initial (minimum) and final (maximum) concrete thicknesses.
Pipeline Outside Diameter – Pipe total outside diameter, including corrosion coating, concrete coating, and marine growth.
Mean Perpendicular Current Velocity – The velocity of the current perpendicular to the pipe, averaged over the pipe diameter.
Significant Flow Velocity Amplitude – The spectrally-derived oscillatory velocity (significant amplitude) for the design spectrum, with the wave spreading and directionality reduction factor applied.
Mean Zero Up-crossing Period – Average period of the zero up-crossing waves, calculated using the zeroth and second moments of the wave spectrum (M₀ and M₂ below, respectively):

T_u=2\pi \sqrt{\frac{M_0}{M_2}}

T_u=2\pi \sqrt{\frac{M_0}{M_2}}

Perpendicular Wave Velocity for Single Design Oscillation – The wave velocity perpendicular to the pipe calculated for a single design oscillation (SDO); derived using the JONSWAP spectral equations, 𝑈^∗.
Period Associated with Single Design Oscillation – Period of the wave associated with a single design oscillation, 𝑇^∗.
Wave Spreading Reduction Factor – The reduction factor applied to the significant flow velocity to account for the effect of main wave directionality and wave spreading. This incorporates projection onto the velocity normal to the pipe and the wave energy spreading directional function.
KC Number for Single Design Oscillation – The Keulegan-Carpenter number for a single design oscillation; calculated using wave velocity of single design oscillation and the period associated with it.

K^=\frac{U^ \cdot T^*}{D}

K^*=\frac{U^* \cdot T^*}{D}

Steady to Oscillatory Velocity Ratio for Single Design Oscillation -The ratio of steady current to oscillatory perpendicular wave velocity for a single design oscillation.

M^=\frac{V^}{U^*}

M^*=\frac{V^*}{U^*}

Pipe Weight Columns – These columns display the weight of the pipe calculated under various conditions, for the respective concrete coating thicknesses in the leftmost column:

• In-air weight of empty pipe
• Submerged weight of empty pipe
• Submerged weight of product-filled pipe (with product density as defined in the Input Data tab)
• Submerged weight of water-filled pipe (with the density of seawater as defined in the Input Data tab)

Total Pipe Penetration – Calculated total pipe penetration for the respective concrete thickness and chosen pipe condition, taken as the summation of the initial penetration and the penetration due to pipe movement:

z_p = z_{pi} + z_{pm}

z_p = z_{pi} + z_{pm} 

Vertical Load Reduction Factor – The reduction factor applied to the vertical force is the product of vertical reduction components for seabed permeability, pipe penetration, and pipe trenching:

r_{tot,z} = r_{perm,z} \cdot r_{pen,z} \cdot r_{tr,z}

r_{tot,z} = r_{perm,z} \cdot r_{pen,z} \cdot r_{tr,z}

Horizontal Load Reduction Factor – The reduction factor applied to the horizontal force is the product of horizontal reduction components for pipe penetration and pipe trenching:

r_{tot,y} = r_{pen,y} \cdot r_{tr,y}

r_{tot,y} = r_{pen,y} \cdot r_{tr,y}

Peak Vertical Load Coefficient – The peak vertical load coefficient is the load coefficient to be multiplied with the peak vertical load, 𝐶_𝑍^∗.
Peak Horizontal Load Coefficient – The peak horizontal load coefficient is the load coefficient to be multiplied with the peak horizontal load, 𝐶_𝑌^∗.
Peak Vertical Hydrodynamic Load – The peak vertical hydrodynamic load for a single design oscillation, 𝐹_𝑍^∗.
Peak Horizontal Hydrodynamic Load – The peak horizontal hydrodynamic load for a single design oscillation, 𝐹_𝑌^∗.
Floating Check UF – The utilization factor (UF) for the pipe floating check; for the pipe to be safe against flotation this value should be less than 1, in accordance with DNV-RP-F109 [2].
Sinking Check UF – The UF for the pipe sinking check; for the pipe to be safe against sinking into the soil this value should be less than 1, in accordance with DNV-RP-F109 [2].
Passive Resistance Parameter – Soil passive resistance parameter calculated for the pipe product-filled submerged weight and maximum lift force (i.e. 𝐹_𝑍^∗ due to a single design oscillation).
Passive Resistance Force -Passive resistance force exerted by the soil on the pipe, calculated based on the passive resistance parameter with condition weight and maximum lift force.
Absolute Static Stability UFs – These are the design criterion utilization factors for absolute lateral static stability, as given in DNV-RP-F109 [2]. For the pipe to satisfy the absolute stability zero displacement criteria, these values should both be less than or equal to 1:

UF_1=\gamma_{sc} \cdot \frac{F_Y^* + \mu \cdot F_Z^}{\mu\cdot \text{w}s + F_R} \leq 1.0\~\ UF_2=\gamma{sc} \cdot\frac{F_Z^}{\text{w}_s} \leq 1.0

UF_1=\gamma_{sc} \cdot  \frac{F_Y^* + \mu \cdot  F_Z^*}{\mu\cdot  \text{w}_s + F_R} \leq 1.0\\~\\ UF_2=\gamma_{sc} \cdot\frac{F_Z^*}{\text{w}_s} \leq 1.0

ASM Reports

Generation of reports for the DNV-RP-F109 ASM analysis is facilitated by the Report toolbar button, and produces a pdf report for saving, as presented in Figure 6-5.

ASM Plots

Generation of graphical information for the DNV-RP-F109 ASM analysis is facilitated by the Plot toolbar button, and produces a graph of the lateral and vertical stability UFs, as presented in Figure 6-6.

References

1. Verley, R. L. P. and Lund, K. M. A Soil Resistance Model for Pipelines Placed on Clay Soils, OMAE – Volume 5, 1995
2. DNV-RP-F109, On-Bottom Stability Design of Submarine Pipelines, Det Norske Veritas, Nov-2011
3. Ochi, M. K. Hubble, E.N. Six-parameter wave spectra, Proceedings 15th International Conference on Coastal Engineering, Honolulu, 1976
4. DNV-OS-F101, Submarine Pipeline Systems, Det Norske Veritas, Oct-2013
5. On-Bottom Stability in Deep Waters Note, Det Norske Veritas
6. Catalog No. L51522e, PR-170-185, Hydrodynamic Forces on Pipelines: Model Tests, Prepared for PRCI by the Danish Hydraulic Institute, Dec-1986
7. PR-170-716, Hydrodynamic Forces Acting on a Pipeline in an Open Trench, Prepared for PRCI by the Danish Hydraulic Institute, Jan-1988
8. Ochi, M. K. and Hubble, E.N. Six-Parameter Wave Spectra, Proceedings 15th International Conference on Coastal Engineering, Honolulu, 1976
9. Mardia, K. V., Statistics of Directional Data. London: Academic Press, 1972
10. Borgman L.E., Directional Wave Spectra from Wave Sensors. In: Earle M.D., Malahoff A. (eds) Ocean Wave Climate. Marine Science, vol 8. Springer, Boston, MA, 1979
11. Mardia, K.V., Some properties of clasical multi-dimesional scaling,Communications in Statistics – Theory and Methods, 1978
12. PR-169-186
13. PR-175-420
14. Catalog No. L51570e, Contract PR-194-719, Energy Based Pipe-Soil Interaction Models, PRCI, June 1988
15. PR-162-157
16. PRCI Project PR-178-04405, Submarine Pipeline On-Bottom Stability Volume 1: Analysis and Design Guidelines, Kellogg Brown & Root, Inc., Dec-2008
17. PRCI Project PR-178-04405, Submarine Pipeline On-Bottom Stability Volume 2: Analysis and Design Guidelines, Kellogg Brown & Root, Inc., Dec-2008
18. Abdolmaleki, K. and Gregory, C. J., Performance of Pipe-Soil Interaction Models in a Quasi-Dynamic Approach to Pipeline Stability Analysis, OMAE-77988, 2018, Spain
19. Jacobsen, V., Bryndum, M.B., and Bonde, C., “Fluid Loads on Pipelines: Sheltered or Sliding,” Proc. 21st Offshore Technology Conference, Paper No. OTC 6056, Houston, 1989

FAQ