AGA 3 – Volume Rate Calculation – Method II

Orifice Flow Equation

The accepted one-dimensional equation for mass flow through a concentric, square edged orifice meter is stated in the Equations below. The derivation is based on conservation of mass and energy, one-dimensional fluid dynamics, and empirical functions such as equations of state and thermodynamic process statements. Any derivation is accurate when all the assumptions used to develop it are valid.

As a result, an empirical orifice plate coefficient of discharge is applied to the theoretical equation to adjust for multidimensional viscous fluid dynamic effects. In addition, an empirical expansion factor is applied to the theoretical equation to adjust for the reduction in fluid density that a compressible fluid experiences when it passes through an orifice plate.

The fundamental orifice meter mass flow equation is as follows: q_m=C_dE_vY(\pi/4)d^2\sqrt{2g_c\rho_{t,p} \Delta P}

q_m=C_dE_vY(\pi/4)d^2\sqrt{2g_c\rho_{t,p} \Delta P}

Where:
𝑞_𝑚 − Mass Flow Rate
𝐶_𝑑−Orifice Plate Coefficient of Discharge
𝑑 − Orifice Plate Bore Diameter (in)
𝐸_𝑣 − Velocity Approach Factor
Δ𝑃 − Orifice Differential Pressure [in 𝐻₂0] at 60℉
𝜋 − Universal Constant = 3.14159
𝑌 − Expansion Factor
𝑔_𝑐 − Dimensional Conversion Factor
𝜌_𝑡,𝑝 − Density of the Fluid at Flowing Conditions (𝑃_𝑓,𝑇_𝑓)

The orifice meter is a mass meter from which a differential pressure signal is developed as a function of the velocity of the fluid as it passes through the orifice plate bore. Manipulation of the density variable in the equation permits calculation of flow rate in either mass or volume units. The volumetric flow rate at flowing (actual) conditions can be calculated using the following equation: q_v=q_m/\rho _{t,p}

q_v=q_m/\rho _{t,p}

The volumetric flow rate at base (standard) conditions can be calculated using the following equation: Q_v=q_m/\rho _b

Q_v=q_m/\rho _b

The mass flow rate (𝑞_𝑚) can be converted to a volumetric flow rate at base (standard) conditions (𝑄_𝑣) if the fluid density at the base conditions (𝜌_𝑏) can be determined or is specified.

Orifice Plate Bore diameter

The orifice plate bore diameter, d. is defined as the diameter at flowing conditions and can be calculated using the following equation: d = d_r \left(1 + \alpha_1(t_f – T_r)\right)

d = d_r \left(1 + \alpha_1(t_f - T_r)\right)

Where:
𝑑 − Orifice Plate Bore Diameter (in)
𝑑_𝑟 − Mean Orifice Bore Diameter (in)
𝛼₁ − Linear Coefficient of Thermal Expansion of Orifice Plate Material (in/in∙℉)
𝑡_𝑓 − Flowing Gas Temperature (℉)
𝑇_𝑟 − Reference Temperature Orifice Plates/Tubes (℉)

The meter tube internal diameter, D, is defined as the diameter at flowing conditions and can be calculated using the following equation: D = D_r \left(1 + \alpha_2(t_f – T_r)\right)

D = D_r \left(1 + \alpha_2(t_f - T_r)\right)

Where;
𝐷 − Meter Tube Internal Diameter (in)
𝐷_𝑟 − Mean Meter Tube Diameter (in)
𝛼₂ − Linear Coefficient of Thermal Expansion of Meter Tube (in/in∙℉)
𝑡_𝑓 − Flowing Gas Temperature (℉)
𝑇_𝑟 − Reference Temperature Orifice Plates/Tubes (℉)

Note: For flowing temperature conditions outside those stated above and for other materials, refer to the American Society for Metals Handbook.
ᵃFor flowing conditions between -100°F and +300°F, refer to ASME PTC 19.5.
ᵇFor flowing conditions between -7°F and + 154°F, refer to API Manual of Petroleum Measurement Standards, Chapter 12, Section 2.

Empirical Coefficient of Discharge Equation for Flange-Tapped Orifice Meters

The concentric, square-edged, flange-tapped orifice meter coefficient of discharge, 𝐶_𝑑(FT), equation, developed by Reader-Harris/Gallagher (RG), is structured into distinct linkage terms and is considered to best represent the current regression data base. The equation is applicable to nominal pipe sizes of 2 inches (50 millimeters) and larger; diameter ratios (𝛽) of 0.1-0.75, provided the orifice plate bore diameter, d” is greater than 0045 inch (11.4 millimeters); and pipe Reynolds numbers (𝑅𝑒_𝐷) greater than or equal to 4000.

C_d = C_i(FT) + 0.000511 \left( \frac{10^6\beta}{Re_D} \right)^{0.7} + (0.0210 + 0.0049A) \beta^4 C \~\
C_i(FT) = C_i(CT) + \text{Tap Term} \~\
C_i(CT) = 0.5961 + 0.2912 \beta^2 – 0.229 \beta^8 + 0.003(1 – \beta) M_1 \~\
\text{Tap Term} = \text{Upstream} + \text{Downstream} \~\
\text{Upstream} = [0.0433 + 0.0712e^{-6.01L_1} – 0.1145e^{-6.01L_1}](1 – 0.23A) B \~\
\text{Downstream} = -0.0116[M_1 – 0.52M_1^{1.3}] \beta^{1.1}(1 – 0.14A)

C_d = C_i(FT) + 0.000511 \left( \frac{10^6\beta}{Re_D} \right)^{0.7} + (0.0210 + 0.0049A) \beta^4 C \\~\\
C_i(FT) = C_i(CT) + \text{Tap Term} \\~\\
C_i(CT) = 0.5961 + 0.2912 \beta^2 - 0.229 \beta^8 + 0.003(1 - \beta) M_1 \\~\\
\text{Tap Term} = \text{Upstream} + \text{Downstream} \\~\\
\text{Upstream} = [0.0433 + 0.0712e^{-6.01L_1} - 0.1145e^{-6.01L_1}](1 - 0.23A) B \\~\\
\text{Downstream} = -0.0116[M_1 - 0.52M_1^{1.3}] \beta^{1.1}(1 - 0.14A)

Where:
𝛽 − Diameter Ratio = 𝑑/D
𝐶_𝑑(𝐹𝑇) − Coefficient of Discharge at a Specific Reynolds number for Flange − Tapped Orifice Meter
𝐶_𝑖(𝐹𝑇) − Coefficient of Discharge at infinite Reynolds number for Flange − Tapped Orifice Meter
𝐶_𝑖(𝐶𝑇) − Coefficient of Discharge infinite Reynolds number for Corner − Tapped Orifice Meter
𝐿₁ − dimensionless correction for the tap location
𝑒 − Napierian Constant = 2.71828
𝑁₄ = 1.0 when D is in Inches = 25.4 when D is in millimeters
𝑅𝑒_𝐷 − pipe Reynolds number

Reynold’s Number

The RG equation uses pipe Reynolds number as the correlating parameter to represent the change in the orifice plate coefficient of discharge, Cd, with reference to the fluid’s mass flow rate (its velocity through the orifice), the fluid density, and the fluid viscosity. The pipe Reynolds number can be calculated using the following equation: Re_D = 0.0114541 \frac{Q_b P_b G_r}{\mu D T_b Z_{bair}}

Re_D = 0.0114541 \frac{Q_b P_b G_r}{\mu D T_b Z_{bair}}

Where:
𝐷 − Meter Tube Internal Diameter (in)
𝑄_𝑏 − Volume Flow Rate at Base Conditions (ft³/hr)
𝑃_𝑏 − Base Pressure
𝑇_𝑏 − Base Temperature (°R)
𝑍_{𝑏𝑎𝑖𝑟} − Compressibility of Air at 14.73 psia and 60℉
μ − Absolute Dynamic Viscosity (lbm/ft³)
𝐺_𝑟 − Real Gas Relative Density
𝑅𝑒_𝐷 − Pipe Reynolds number

Velocity of Approach Factor

The velocity of approach factor, 𝐸_𝑣 , is calculated as follows:

\begin{align} E_v &= \frac{1}{\sqrt{1 – \beta^4}} \~\ \text{And, } \~\ \beta &= \frac{D}{ID} \end{align}

E_v = \frac{1}{\sqrt{1 – \beta^4}} \~\ \text{And,} \~\ \beta = \frac{D}{ID}

\begin{align*}
E_v &= \frac{1}{\sqrt{1 - \beta^4}} \\~\\
\text{And, } \\~\\
\beta &= \frac{D}{ID}
\end{align*}

Where:
𝛽 − Diameter Ratio
𝐸_𝑣 − Velocity Approach Factor
𝑑 − Orifice Plate Bore Diameter (in)
𝐷 − Meter Tube Internal Diameter (in)

This assumption defines the expansion as reversible and adiabatic (no heat gain or loss). Within practical operating ranges of differential pressure, flowing pressure, and temperature, the expansion factor equation is insensitive to the value of the isentropic exponent. As a result, the assumption of a perfect or ideal isentropic exponent is reasonable for field applications.

The application of the expansion factor is valid if the following dimensionless pressure ratio criteria are followed:

\begin{align} 0&<\frac{\Delta P}{N_3P_{f1}}<0.2 \~\ \text{or, } \~\ 0.8&<\frac{P_{f2}}{P_{f1}}<1.0 \end{align}

\begin{align*}
0&<\frac{\Delta P}{N_3P_{f1}}<0.2 \\~\\
\text{or, } \\~\\
0.8&<\frac{P_{f2}}{P_{f1}}<1.0
\end{align*}

Where:
𝑁₃ − Unit Conversion Factor
𝑃_𝑓1 − Absolute Static Pressure at Upstream Tap (psi)
𝑃_𝑓2 − Absolute Static Pressure at Downstream Tap (psi)
Δ𝑃 − Orifice Differential Pressure (in 𝐻₂0) at 60℉

Upstream/Downstream Expansion Factor

The upstream expansion factor requires determination of the upstream static pressure, the diameter ratio, and the isentropic exponent. If the absolute static pressure is taken at the upstream differential pressure tap, then the value of the expansion factor, 𝑌₁ , shall be calculated as follows: Y_1 = 1 – \left(0.3625 + 0.1027 \beta^4 + 1.1328 \beta^8\right) \left[1 – \left(1 – x_1\right)^{\frac{1}{k}}\right]

Y_1 = 1 - \left(0.3625 + 0.1027 \beta^4 + 1.1328 \beta^8\right) \left[1 - \left(1 - x_1\right)^{\frac{1}{k}}\right]

When the upstream static pressure is measured, : x_1=\frac{\Delta P}{N_3P_{f1}}

x_1=\frac{\Delta P}{N_3P_{f1}}

When the downstream static pressure is measured, : x_1=\frac{\Delta P}{N_3P_{f2}+\Delta P}

x_1=\frac{\Delta P}{N_3P_{f2}+\Delta P}

Where:
𝑌₁ − Upstream Expansion Factor
𝑁₃ − Unit Conversion Factor
𝑥₁ − Ratio of Differential Pressure to Absolute Static Pressure
𝑃_𝑓1 − Absolute Static Pressure at Upstream Tap (psi)
𝑃_𝑓2 − Absolute Static Pressure at Downstream Tap (psi)
Δ𝑃 − Orifice Differential Pressure [in 𝐻₂0]at 60℉
𝑘 − Isentropic Exponent
𝛽 − Diameter Ratio

The downstream expansion factor requires determination of the downstream static pressure, the upstream static pressure, the downstream compressibility factor, the upstream compressibility factor, the diameter ratio, and the isentropic exponent. The value of the downstream expansion factor, 𝑌₂, shall be calculated using the following equation: Y_2 = \left[ 1 – \left(0.3625 + 0.1027\beta^4 + 1.1328\beta^8\right) \biggl{ 1 – \left(1 – x_1\right)^{\frac{1}{k}}\biggl} \right] \sqrt{\frac{P_{f1} Z_{f2}}{P_{f2} Z_{f1}}}

Y_2 = \left[ 1 - \left(0.3625 + 0.1027\beta^4 + 1.1328\beta^8\right) \biggl\{ 1 - \left(1 - x_1\right)^{\frac{1}{k}}\biggl\} \right] \sqrt{\frac{P_{f1} Z_{f2}}{P_{f2} Z_{f1}}}

When the upstream static pressure is measured, : x_1=\frac{\Delta P}{N_3P_{f1}}

x_1=\frac{\Delta P}{N_3P_{f1}}

When the downstream static pressure is measured, : x_1=\frac{\Delta P}{N_3P_{f2}+\Delta P}

x_1=\frac{\Delta P}{N_3P_{f2}+\Delta P}

Where:
𝑌₁ − Upstream Expansion Factor
𝑌₂ − Downstream Expansion Factor
𝑁₃ − Unit Conversion Factor
𝑥₁ − Ratio of Differential Pressure to Absolute Static Pressure
𝑥₁/𝑘 − Upstream Acoustic Ratio
𝑃_𝑓1 − Absolute Static Pressure at Upstream Tap (psi)
𝑃_𝑓2 − Absolute Static Pressure at Downstream Tap (psi)
𝑍_𝑓1 − Fluid Compressibility at Upstream Tap (psi)
𝑍_𝑓2 − Fluid Compressibility at Downstream Tap (psi)
Δ𝑃 − Orifice Differential Pressure (in 𝐻₂0) at 60℉
𝑘 − Isentropic Exponent
𝛽−Diameter Ratio

Supercompressibility

In orifice measurement, 𝑍_𝑏 and 𝑍_𝑓1 appear as a ratio to the 0.5 power. This relationship is termed the supercompressibility factor and may be calculated from the following equation: F_{pv}=\sqrt{\frac{Z_b}{Z_{f1}}}

F_{pv}=\sqrt{\frac{Z_b}{Z_{f1}}}

Base Pressure Factor

If contract base pressure differs from the reference base conditions (14.73 psia and 60℉), the initial calculated flow rate at reference base conditions will require conversion to the flow rate at the given base conditions. :F_{pb}=14.73psia /P_b

F_{pb}=14.73psia /P_b

Base Temperature Factor

If contract base temperature differs from the reference base conditions (14.73 psia and 60℉), the initial calculated flow rate at reference base conditions will require conversion to the flow rate at the given base conditions. :F_{tb} = T_b/{519.67\,^{\circ}R}

F_{tb} = T_b/{519.67\,^{\circ}R}

Flowing Temperature Factor

F_{tf} = \sqrt{\frac{519.67\,^{\circ}R}{T_f}}

F_{tf} = \sqrt{\frac{519.67\,^{\circ}R}{T_f}}

Real Gas Relative Density Factor

F_{gr}=\sqrt{\frac{1}{G_r}}

F_{gr}=\sqrt{\frac{1}{G_r}}

Numeric Conversion Factor

F_n=338.196E_v(D^2)(\beta^2)

F_n=338.196E_v(D^2)(\beta^2)

Flow Rate at Standard Conditions

Q_v = F_n \left(F_c + F_{st}\right) Y_1 F_{pb} F_{tb} F_{tf} F_{gr}F_{pv} F_{zb} \sqrt{{P_{f1} \Delta P}}

Q_v = F_n \left(F_c + F_{st}\right) Y_1 F_{pb} F_{tb} F_{tf} F_{gr}F_{pv} F_{zb} \sqrt{{P_{f1} \Delta P}}

Flow Rate at Base Conditions

Q_b = Q_v \left(\frac{P_s}{P_b}\right) \left(\frac{T_b}{T_s}\right) \left(\frac{Z_b}{Z_s}\right)

Q_b = Q_v \left(\frac{P_s}{P_b}\right) \left(\frac{T_b}{T_s}\right) \left(\frac{Z_b}{Z_s}\right)

Case Guide

Part 1: Create Case

Input Parameters

• Operating Temperature (℉)
• Operating Pressure (psig)
• Base Temperature (℉)
• Base Pressure (psig)
• Static Pressure Measurements (Upstream/Downstream)
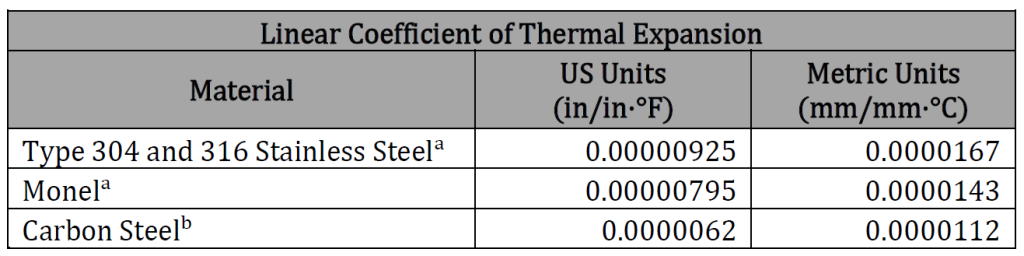
• Linear Coefficient of Thermal Expansion
  • Orifice AGA
  • Meter Tube
• Reference Temperature Orifice Plates/Tube (℉)
• Compressibility Factor at Flowing Conditions
• Compressibility Factor at Base Conditions
• Compressibility Factor at Standard Conditions
• Mean Orifice Bore Diameter (in)
• Mean Meter Tube Internal Diameter (in)
• Real Gas Relative Density
• Differential Pressure [in H₂O] at 60 deg F
• Carbon Dioxide (%)
• Nitrogen (%)
• Gas Dynamic Viscosity (lb/ft-sec)
• Isentropic Exponent

Upstream Tap

Downstream Tap

Part 2: Outputs/Reports

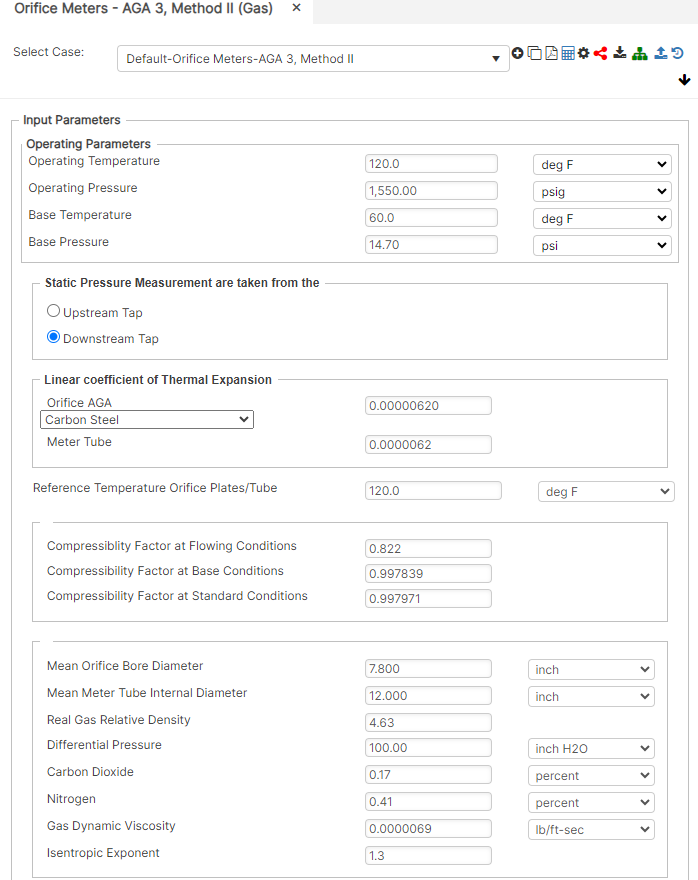
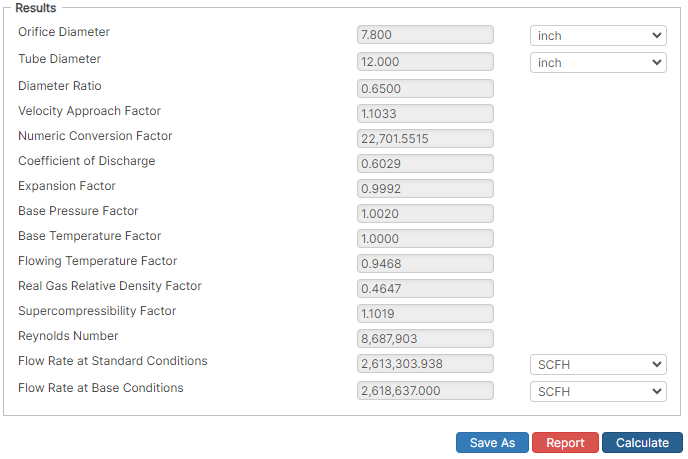
Results

• Orifice Diameter (in)
• Tube Diameter (in)
• Diameter Ratio
• Velocity Approach Factor
• Velocity Approach Factor
• Numeric Conversion Factor
• Coefficient of Discharge
• Expansion Factor
• Base Pressure Factor
• Base Temperature Factor
• Flowing Temperature Factor
• Real Gas Relative Density Factor
• Super compressibility Factor
• Reynolds Number
• Flow Rate at Standard Conditions (SCFH)
• Flow Rate at Base Conditions (SCFH)

Upstream Tap

Downstream Tap

References

• AGA Report No. 3 – Orifice Metering of Natural Gas and other Related Hydrocarbon Fluid – Parts 1-4