API 1117 – Movement of In-Service Pipeline (Liquid)

Contents

Introduction

Movement of in-service Pipelines is calculated to conform elastically to a given trench profile. Longitudinal Stress due to bending/elongation and elastic curvature must be considered.

Total Longitudinal Stress

The total longitudinal stress in the pipe can be estimated with the following equation: S_L=S_E+S_B+S_S

S_L=S_E+S_B+S_S

Where:
𝑆_𝐿= Total Longitudinal Stress in the Pipe (psi)
𝑆_𝐸= Existing Longitudinal Stress in the Pipe (psi)
𝑆_𝐵 = Longitudinal Stress in the Pipe due to Bending caused by Movement Operation (psi)
𝑆_𝑆 = Longitudinal Stress in the Pipe due to its Elongation caused by the Movement Operation (psi)

Longitudinal Tensile Stress Due To Internal Pressure

The longitudinal tensile stress in the pipe due to internal pressure may be estimated with the following equation: S_P=\frac{PD\mu}{2t}

S_P=\frac{PD\mu}{2t}

Where:
𝑆𝑃 = Longitudinal Tensile Stress in the Pipe due to Internal Pressure (psi)
𝑃 = Maximum Internal Operating Pressure of the Pipe (psi)
𝐷 = Outside Diameter of the Pipe (in)
𝜇 = Poisson′s Ratio for Steel − (0.3)
𝑡 = Nominal Wall Thickness of the Pipe (in)

Longitudinal Tensile Stress Due To Temperature Change

The longitudinal tensile stress in the pipe due to a change in the temperature may be estimated with following equation: S_r=E\alpha(T_1-T_2)

S_r=E\alpha(T_1-T_2)

Where:
𝑆_𝑟 = Longitudinal Tensile Stress in the Pipe due to Change in Temperature (psi)
𝐸 = Modulus of Elasticity of Steel − 29×10⁶
𝛼 = Linear Coefficient of Thermal Expansion for Steel − 6.5×10⁻⁶ (in/℉)
𝑇₁ = Temperature of the Pipe at Installation (℉)
𝑇₂ = Operating Temperature of the Pipe during Movement (℉)
*If the pipe’s temperature at installation time is not known, it should be reasonably estimated*

Longitudinal Flexure Stress Due To Existing Elastic Curvature

When a pipeline is laid to conform elastically to a given trench profile, the pipeline will experience induced flexural stress in amount proportional to its curvature. In hilly terrain, where slopes are unstable, or where soils are subject to frost heave or liquefaction, the pipeline is likely to experience stress of unpredictable and varying magnitude. This stress 𝑆_𝐶 )can range from near-yield-strength levels in tension to near-bulking levels in compression. This existing stress should be considered prior to a movement operation.

Existing Longitudinal Stress

The existing longitudinal stress in a pipeline will normally be in the range of-10,000 psi to 20,000 psi. In the flat or gently rolling terrain where soils are not subject to frost heave or liquefaction, the pipeline will experience only the longitudinal tensile stress due to internal pressure and temperature as discussed above. The existing longitudinal stress in the pipe may be estimated
With following equation: S_E=S_p+S_r+S_c

S_E=S_p+S_r+S_c

Where:
𝑆_𝐶 = Longitudinal Tensile Stress in the Pipe due to Existing Elastic Curvature (psi)

Longitudinal Stress Due To Bending

The longitudinal stress in the pipe due to bending may be estimated with following equation: S_B=\frac{w_rL_I^2}{12S}

S_B=\frac{w_rL_I^2}{12S}

Where:
𝑤_𝑟 = Net uniformly distributed load required to achieve the desired mid-span vertical deflection of the pipe (not full weight of the pipe and fluid) (psi)
𝐿_𝐼 = Minimum trench length required to reach the mid-span vertical deflection of the Pipe (in)
𝑆 = Elastic section modulus of the pipe (in)

Longitudinal Stress Due To Elongation

The longitudinal stress in the pipe due to elongation caused by the movement operation may be estimated with the following equation: S_S=2.67E\left( \frac{\Delta}{L}\right)^2

S_S=2.67E\left( \frac{\Delta}{L}\right)^2

Where:
Δ = Mid-span deflection of the pipe, (ft)
𝐿 = Minimum trench length required to reach the mid-span deflection of the pipe Δ (ft)
*The effects of this stress may be offset by an elastic compressive stress existing in the pipeline prior to the moving because of slack*

Available Longitudinal Bending Stress

The longitudinal stress available for bending may be estimated with the following equation: S_A=F_DSMYS-S_E-S_S

S_A=F_DSMYS-S_E-S_S

Where:
𝑆_𝐴 = Longitudinal stress available for bending (psi)
𝐹_𝐷 = Design Factor
SMYS = Specific Minimum Yield Strength (psi)

Trench Length

The minimum trench length required to achieve a mid-span deflection of the pipe without exceeding the longitudinal stress limit can be determined with the following equation, based on elastic free deflection theory, which treats the pipe as a single-span beam that is fixed at both ends and that has a uniformly distributed load: L = \sqrt{\frac{(3.87 \times 10^7) D\Delta (7.74 \times 10^7) \Delta^2}{F_D SMYS – S_E}}

L = \sqrt{\frac{(3.87 \times 10^7) D\Delta (7.74 \times 10^7) \Delta^2}{F_D SMYS - S_E}}

Trench (Or Displacement) Profile

A profile for the moved portion of the pipeline should be designed to minimize induced bending stress concentrations. Therefore, to obtain acceptable longitudinal stress distribution due to bending, the deflection at any point along the trench profile can be determined with the following equation: \Delta_x = \frac{16X^2 \Delta (L – x)^2}{L^4}

\Delta_x = \frac{16X^2 \Delta (L - x)^2}{L^4}

Where:
Δ𝑥 = Vertical Deflection of the Pipe at Distance x (ft)
L = longitudinal stress available for bending (psi)
𝑥 = Distance along the length of the trench from the starting point of the pipe deflection (ft)

Supporting Spacing

Based on a four-span, uniformly loaded beam, the maximum free span between supports can be determined with the following equation: L_s = \sqrt{\frac{0.0286S_A (D^4 – d^4)}{D^3 – 0.8724d^2D}}

L_s = \sqrt{\frac{0.0286S_A (D^4 - d^4)}{D^3 - 0.8724d^2D}}

Where:
𝐿𝑆 = Maximum Free Span Between Pipe Supports (ft)
𝑑 = Inside Diameter of the Pipe (in)

Case Guide

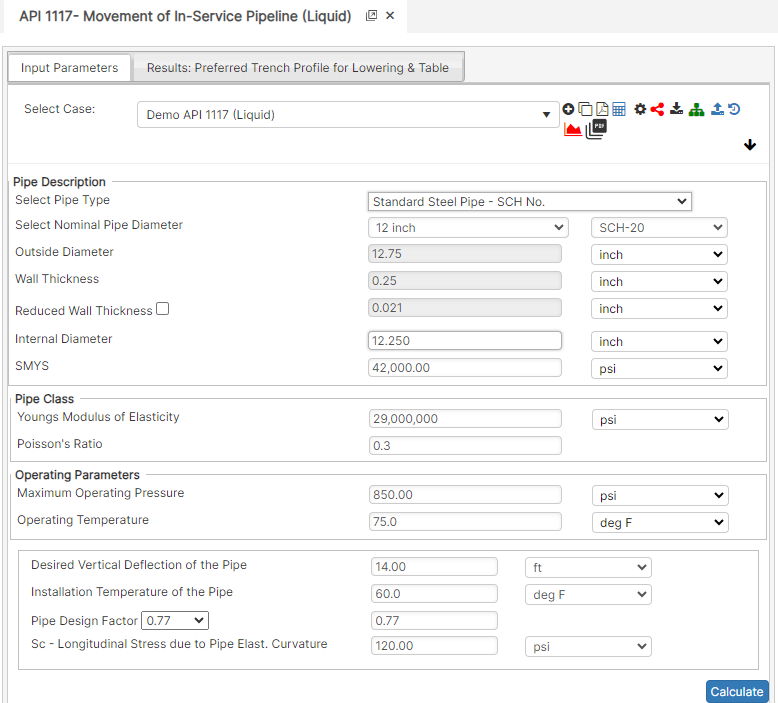
Part 1: Create Case

Select the API 1117 – Movement of In-Service Pipeline application from the PLTB Misc. Module
To create a new case, click the “Add Case” button
Enter Case Name, Location, Date and any necessary notes.
Fill out all required Parameters.
Make sure the values you are inputting are in the correct units.
Click the CALCULATE button to overview results.

Input Parameters

Nominal Pipe Size
Outside Pipe Diameter (in)
Pipe Wall Thickness (in)
Internal Pipe Diameter (in)
Specified Minimum Yield Strength (psi)
Modulus of Elasticity of Steel (psi)
Poisson’s Ratio for Steel
Maximum Operating Pressure (psi)
Operating Temperature of the Pipe (°F)
Desired Vertical Deflection of the Pipe (ft)
Installation Temperature of the Pipe (°F)
Pipe Design Factor
Sc – Longitudinal Stress due to Pipe Elasticity Curvature (psi)

Part 2: Outputs/Reports

If you need to modify an input parameter, click the CALCULATE button after the change.
To SAVE, fill out all required case details then click the SAVE button.
To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
To generate a REPORT, click the REPORT button.
The user may export the Case/Report by clicking the Export to Excel icon.
To delete a case, click the DELETE icon near the top of the widget.

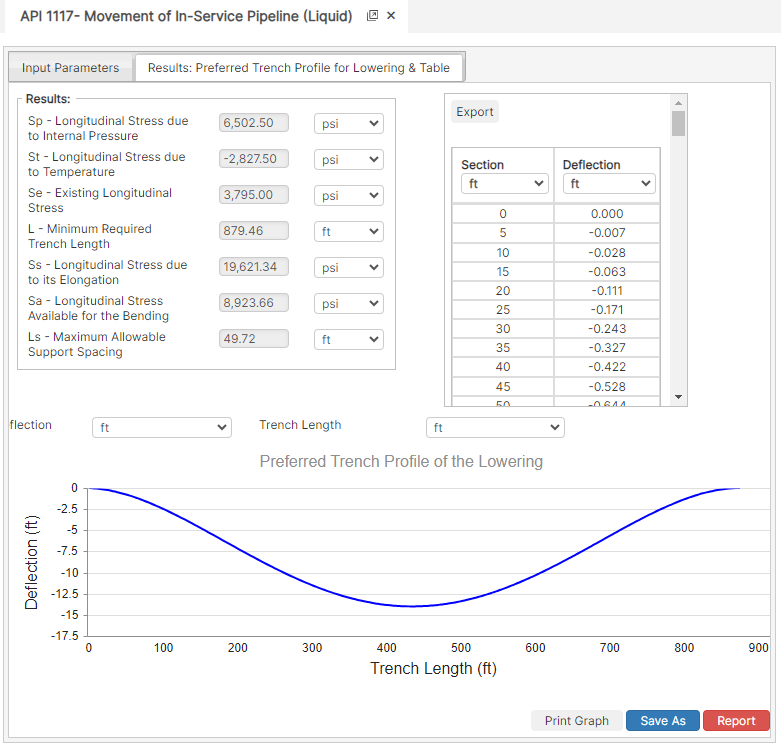
Results

Sp – Longitudinal Stress due to Internal Pressure (psi)
St – Longitudinal Stress due to Temperature (psi)
Se – Existing Longitudinal Stress (psi)
L – Minimum Required Trench Length (ft)
Ss – Longitudinal Stress due to its Elongation (psi)
Sa – Longitudinal Stress Available for the Bending (psi)
Ls – Maximum Allowable Support Spacing (ft)
Deflection (ft)
Trench Length (ft)

References

API 1117 – Recommended Practice for Movement of In-Service Pipelines

Updated on January 4, 2024

Tagged: Calculations Miscellaneous - Liquid

Was this article helpful?

Yes No