CEPA Wheel Load Analysis

Introduction

The Track Load Program was designed to calculate the overburden and track loads on buried pipe with a Single Layer System (soil only). The information used to design this program was taken from the Newmark’s Integration of the Boussinesq Equation which considered the theoretical work done by M.G. Spangler on overburden and vehicle loads on buried pipe. This analysis does not evaluate cyclic loading, but the API 1102 calculation does.

Variables and Boundary Conditions

REQUIRED INFORMATION:

1. Values for all the following variables:

2. Variables for the following information about the track:

• 𝐿_𝑡 − Operating Weight of the Object Crossing the Pipeline with Tracks(lbs)
• 𝑇_𝑤 − Width of the Standard Track Shoe(in)
• 𝑇_𝑙 − Length of the Track on the Ground(ft)
• 𝑇_𝑔 − Track Gauge(ft)

Note: To find loaded & unloaded vehicles and construction equipment specifications and dimensions, use https://www.ritchiespecs.com/ for this information.

3. The Design Factor of the pipeline being analyzed is used to find the Maximum Allowable Combined Stress (% SMYS), (0.72 is the standard factor used for liquid).
4. The Soil Type which is used to find the friction force coefficients (Km), see Table II.
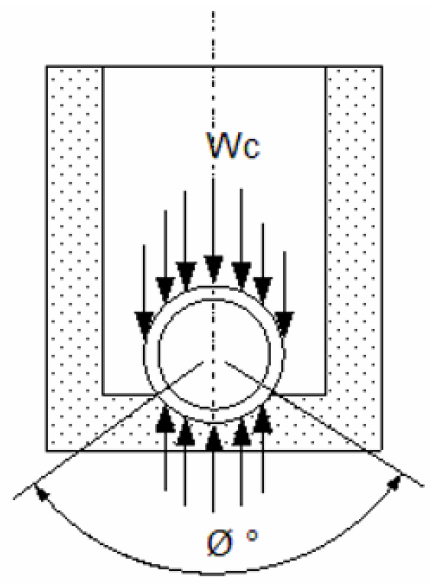
5. The Crossing Construction Type which is used to find the bedding constants for buried pipe (Kb & Kz), see Table V & Figure 3.

6. All the above information along with values for the following variables:

• X – Longitudinal Distance over which Deflection Occurs (ft)
• Y – Vertical Deflection (in)

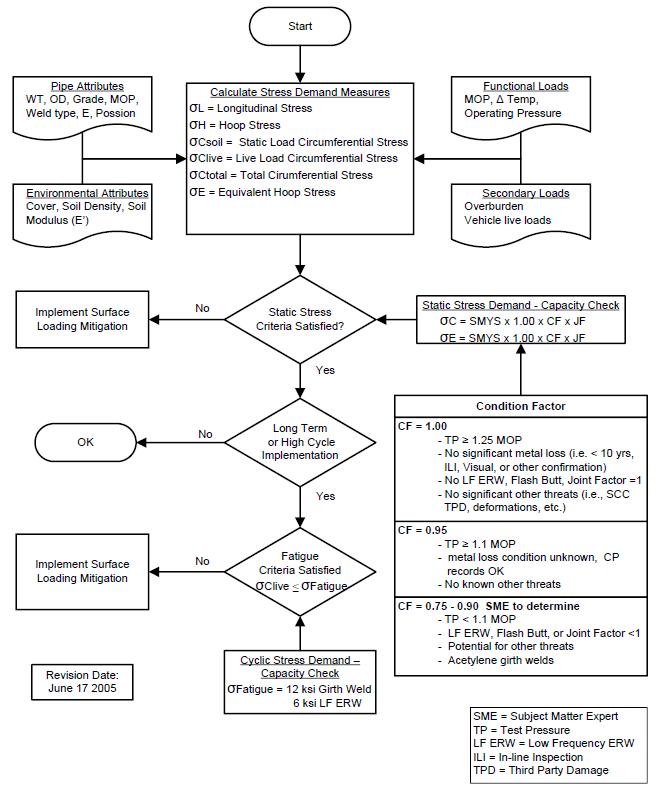
Workflow

Pipeline Surface Load Acceptability Process: 

The pressure exerted on the pipe at pipeline depth due to a load at the surface can be calculated using Boussinesq’s equation: 

(1)

P_{\text{live}} = \frac{W_{\text{live}}}{D} = \frac{3 \cdot F}{2 \pi H^2 \left[1 + \left(\frac{d}{H}\right)^{2}\right]^{2.5}}

P_{\text{live}} = \frac{W_{\text{live}}}{D} = \frac{3 \cdot F}{2 \pi H^2 \left[1 + \left(\frac{d}{H}\right)^{2}\right]^{2.5}}

Where:

• P_live = Pressure on the pipe due to the live load (psi) 
• W_live = Live load on the pipe (lb/in) 
• D = Diameter of the pipe (in) 
• F = Point load at the surface (lb) 
• H = Depth of soil cover (in) 
• d = Offset distance from the pipe to the line of application of the surface load (in) 

Using this equation, a tire, track, or any other load with a known contact area can be represented by a series of point loads at the surface, and the total load on the pipe is calculated as the summation of the effect of the individual loads. 

The CEPA equation combines the pressure stiffening and soil restraint terms into a single equation for determining circumferential (hoop) bending stresses due to live or soil loads: 

(2)

\sigma_{H_live} = \frac{3 \cdot K_b \cdot P_{\text{live}}\cdot \left(\frac{D}{t}\right)^2}{1 + 3 \cdot K_z\cdot \frac{P}{E} \cdot\left(\frac{D}{t}\right)^3 + 0.0915 \cdot \frac{E’}{E}\cdot \left(\frac{D}{t}\right)^3}

\sigma_{H\_live} = \frac{3 \cdot K_b \cdot P_{\text{live}}\cdot \left(\frac{D}{t}\right)^2}{1 + 3 \cdot K_z\cdot \frac{P}{E} \cdot\left(\frac{D}{t}\right)^3 + 0.0915 \cdot \frac{E'}{E}\cdot \left(\frac{D}{t}\right)^3}

Where: 

• σ_{H_live}= circumferential (hoop) bending stress due to the live load (psi) 
• K_b = Soil parameter 
• t = Wall thickness (in) 
• K_z = Soil parameter 
• P = Internal pressure (psig) 
• E = Young’s modulus of elasticity for steel (30×106 psi) 
• E’ = Modulus of soil reaction (psi) 

and 

(3)

\sigma_{H_soil} = \frac{3 \cdot K_b \cdot P_{\text{soil}}\cdot \left(\frac{D}{t}\right)^2}{1 + 3 \cdot K_z\cdot \frac{P}{E} \cdot\left(\frac{D}{t}\right)^3 + 0.0915 \cdot \frac{E’}{E}\cdot \left(\frac{D}{t}\right)^3}

\sigma_{H\_soil} = \frac{3 \cdot K_b \cdot P_{\text{soil}}\cdot \left(\frac{D}{t}\right)^2}{1 + 3 \cdot K_z\cdot \frac{P}{E} \cdot\left(\frac{D}{t}\right)^3 + 0.0915 \cdot \frac{E'}{E}\cdot \left(\frac{D}{t}\right)^3}

Where: 

• σ_{H_soil} = Circumferential (hoop) bending stress due to the soil load (psi) 

The circumferential (hoop) stress due to internal pressure is given as: 

(4)

\sigma_{H_internal}=\frac{P\cdot D}{2\cdot t}

\sigma_{H\_internal}=\frac{P\cdot D}{2\cdot t}

Where: 

• σ_{H_internal} = Circumferential (hoop) stress due to internal pressure (psi) 

The total circumferential stress, , is the sum of the stresses due to circumferential bending along with the hoop stress due to internal pressure.  The total circumferential stress is compared to the allowable limit. 

Internal pressure in pipelines restrained in soil causes a longitudinal stress equal to: 

(5)

\sigma_{L_internal}=v\cdot\sigma_{H_internal}

\sigma_{L\_internal}=v\cdot\sigma_{H\_internal}

Where:

• σ_{L_internal} = Longitudinal stress due to internal pressure (psi) 

• v = Poisson’s ratio for steel (0.3) 

In a manner similar to the longitudinal stress from pressure, the soil load causes a longitudinal stress equal to: 

(6)

\sigma_{L_soil}=v\cdot\sigma_{H_soil}

\sigma_{L\_soil}=v\cdot\sigma_{H\_soil}

Where: 

• σ_{L_soil} = Longitudinal stress due to soil load (psi) 

The longitudinal stress due to the live load is determined as a combination of stress due to local bending and beam deflection.  The calculation for the local longitudinal stress caused by the surface load is estimated using Bjilaard’s solutions for local loading on a pipe found in Roark’s Formulas for Stress and Strain.

(7)

\sigma_{L_{local}} = \frac{0.153}{1.56} \cdot \beta^{4} \cdot \sigma_{H_{live}}

\sigma_{L\_{local}} = \frac{0.153}{1.56} \cdot \beta^{4} \cdot \sigma_{H\_{live}}

Where: 

• σ_{L_local} = local bending stress (psi) 

and 

(8)

\beta = \left[12 \cdot (1 – v^{2})\right]^{1/8}

\beta = \left[12 \cdot (1 - v^{2})\right]^{1/8}

The vehicle load causes an axial pipeline deflection, which adds to the longitudinal stress due to internal pressure and temperature differential.  If the pipeline is modeled as a beam on an elastic foundation, the maximum bending moment is given by Hetenyi1 as: 

(9)

M = \frac{P_{\text{pipe}} \cdot D}{4\lambda^2} (2e^{-\lambda x} \sin \lambda x)

M = \frac{P_{\text{pipe}} \cdot D}{4\lambda^2} (2e^{-\lambda x} \sin \lambda x)

Where: 

• M = Bending moment (in-lb) 
• P_pipe = Pressure on pipe from an equivalent point load (psi) 
• λ = Characteristic length (in-1) 
• x = Distance along the pipeline (in) 

and 

(10)

\lambda = \sqrt[4]{\frac{E’ \cdot D \cdot \theta}{4 \cdot E \cdot I}}

\lambda = \sqrt[4]{\frac{E' \cdot D \cdot \theta}{4 \cdot E \cdot I}}

Where: 

• Ө = Bedding angle of pipe (degrees) 

• λ = Pipe moment of inertia (in4) 

This is the uniformly distributed pressure on the pipe due to an equivalent point load at the surface that spreads at the soil distribution angle of 29.9 degrees from the surface point. 

The longitudinal bending stress is given as: 

(11)

\sigma_{L_bend}=\frac{M\cdot D}{2I}

\sigma_{L\_bend}=\frac{M\cdot D}{2I}

Where: 

• σ_{L_bend} = Longitudinal bending stress (psi) 

The total longitudinal stress due to temperature differential is given as: 

(12)

\sigma_{L_thermal}=E\cdot \alpha\cdot \Delta T

\sigma_{L\_thermal}=E\cdot \alpha\cdot \Delta T

Where: 

• σ_{L_thermal} = Longitudinal thermal stress (psi) 
• α = Coefficient of thermal expansion for steel (6.67×10-6 in/in deg F) 
• △T = Temperature differential (installation – operation) 

The total longitudinal stress, , is the sum of the stresses from internal pressure, soil load, surface loads, axial deflection, and temperature differential.  The total longitudinal stress is compared to the allowable limit. 

The combined equivalent (Tresca – Equation 14; von Mises – Equation 15) stress is calculated as: 

(13)

\sigma_{E} = \max(|\sigma_{H_{Total}}|, |\sigma_{L_{Total}}|, |\sigma_{H_{Total}} – \sigma_{L_{Total}}|)

\sigma_{E} = \max(|\sigma_{H\_{Total}}|, |\sigma_{L\_{Total}}|, |\sigma_{H\_{Total}} - \sigma_{L\_{Total}}|)

(14) 

\sigma_{E} = \sqrt{\sigma_{H_{Total}}^2 – \sigma_{H_{Total}} \cdot \sigma_{L_{Total}} + \sigma_{L_{Total}}^2}

\sigma_{E} = \sqrt{\sigma_{H\_{Total}}^2 - \sigma_{H\_{Total}} \cdot \sigma_{L\_{Total}} + \sigma_{L\_{Total}}^2}

Where: 

• σ_E = Combined equivalent stress (psi) 

Case guide

Part 1: Create Case

Input Parameters

• Nominal Pipe Size(in):(1/8” – 48”)
• Pipe Outside Diameter(in):(0.625” – 48”)
• Pipe Wall Thickness(in):(0.068”- >2”)
• Pipe Grade
• SMYS
• Pipe Regularly Code
• Location Class
• Design Factor
• Youngs Modulus of Elasticity
• Poisson’s Ratio
• Coefficient of Thermal Expansion
• Maximum Operating Pressure
• Operating Temperature
• Pipe Installation Temperature

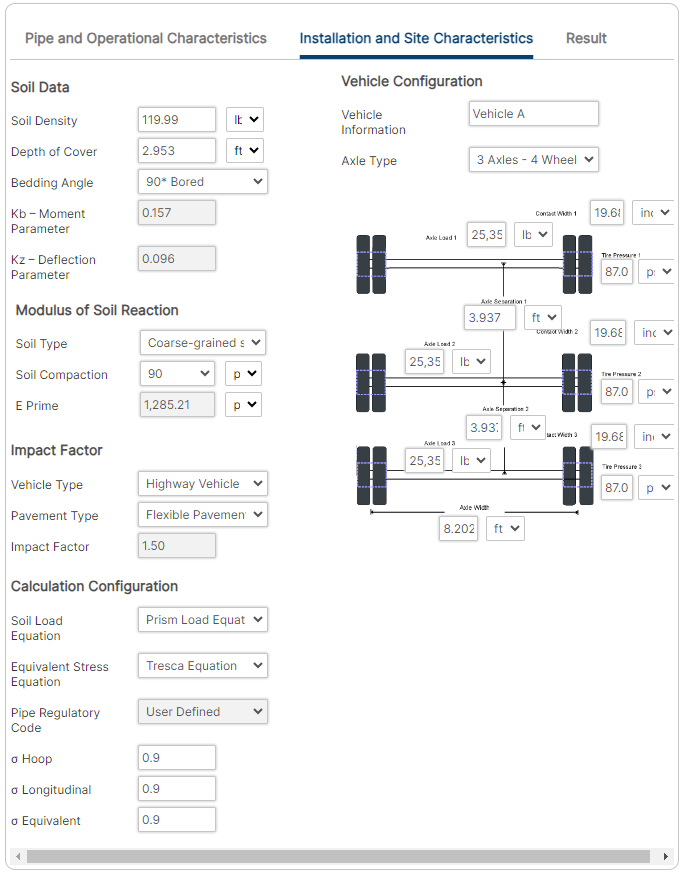
Installation and Site Characteristics:

• Soild Density 
• Depth of Cover
• Bedding Angle
• Kb – Moment Parameter
• Kz – Deflection Parameter
• Soil Type
• Soil Compaction
• E Prime
• Vehicle Type
• Pavement Type
• Impact Factor
• Soil Load Equation
• Equivalent Stress Equation
• Pipe Regulatory Code
• Stress – Hoop
• Stress – Longitudinal
• Stress – Equivalent
• Vehicle Information
• Axle Type
• Axle Load 1
• Contact Width 1
• Tire Pressure 1
• Axle Separation
• Axle Load 2
• Contact Width 2
• Tire Pressure 2
• Axle Width

Part 2: Outputs/Reports

Results

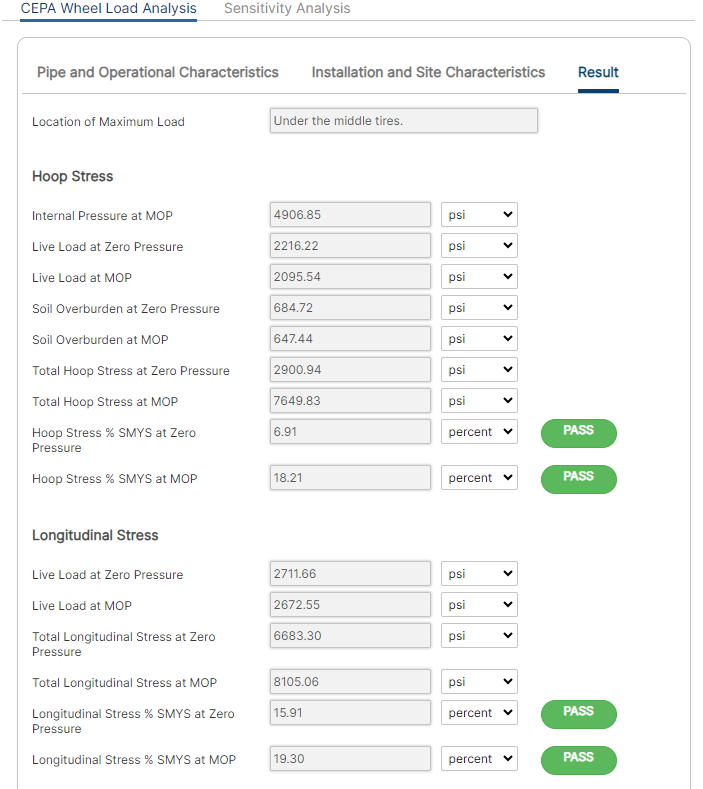
Hoop Stress:

• Internal Pressure at MOP
• Live Load at Zero Pressure
• Live Load at MOP
• Total Hoop Stress at Zero Pressure
• Total Hoop Stress at MOP
• Hoop Stress % SMYS at Zero Pressure
• Hoop Stress % SMYS at MOP

Longitudinal Stress:

• Live Load at Zero Pressure
• Live Load at MOP
• Total Longitudinal Stress at Zero Pressure
• Total Longitudinal at MOP
• Longitudinal Stress % SMYS at Zero Pressure
• Longitudinal Stress % at MOP

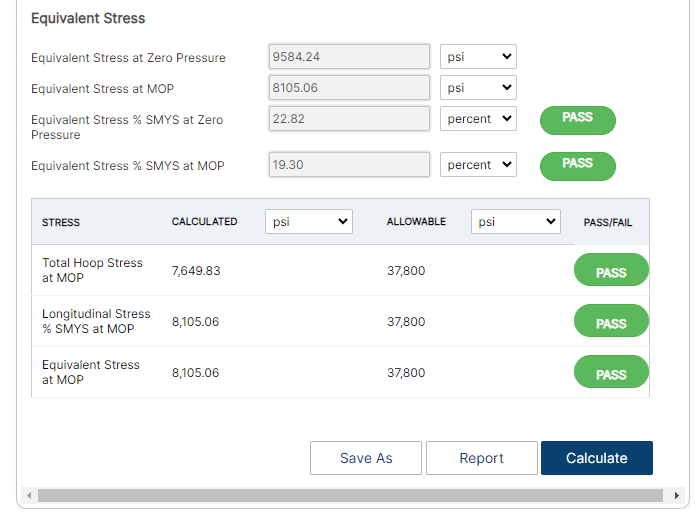
Equivalent Stress:

• Equivalent Stress at Zero Pressure
• Equivalent Stress at MOP
• Equivalent Stress % SMYS at Zero Pressure
• Equivalent Stress % SMYS at MOP

Results Table: 

• Total Hoop Stress @ MOP
• Longitudinal Stress % SMYS @ MOP
• Equivalent Stress @ MOP

Reference

• “Canadian Energy Pipeline Association (CEPA) “Development of a Pipeline Surface Loading Screening Process and Assessment of Surface Load Dispersing Methods”, October 2009

FAQ