Searching...
  1. Home
  2. Our Products
  3. Pipeline Toolbox
  4. Hydraulics
  5. Gas
  6. Colebrook – White (Gas)

Colebrook – White (Gas)

Contents

Introduction

The Colebrook-White equation is recommended for use by those unfamiliar with pipeline flow equations. It will produce the greatest consistency of accuracy over the widest possible range of variables. The Colebrook Equation has good accurate results for lower flow rates (150-250 MMSCFD); However, larger errors exist above a 250 MMSCFD flow rate.

The friction factor is solved using the Newton-Raphson method.

f=\frac{64}{Re};\,Laminar\,Flow: Re < 2000 \~\ \frac{1}{\sqrt{f}}=2\log_{10}(Re\sqrt{f})-0.8;\,Smooth\,Pipe:Re >4000\,and\,\frac{\varepsilon}{D}\rightarrow0\~\ \frac{1}{\sqrt{f}}=-2\log_{10}\biggr(\frac{\varepsilon}{3.7D}+\frac{2.51}{Re\sqrt{f}}\biggr);\,Transitional,\,Colebrook-White\,Eq,Re>4000\~\ \frac{1}{\sqrt{f}}=1.14-2\log_{10}\biggr(\frac{\varepsilon}{D}\biggr);\,Wholly \,Rough

f=64Re; Laminar Flow:Re<2000 1f=2log⁡10(Ref)−0.8; Smooth Pipe:Re>4000 and εD→0 1f=−2log⁡10(ε3.7D+2.51Ref); Transitional, Colebrook−White Eq,Re>4000 1f=1.14−2log⁡10(εD); Wholly Roughf=\frac{64}{Re};\,Laminar\,Flow: Re < 2000 \\~\\ \frac{1}{\sqrt{f}}=2\log_{10}(Re\sqrt{f})-0.8;\,Smooth\,Pipe:Re >4000\,and\,\frac{\varepsilon}{D}\rightarrow0\\~\\ \frac{1}{\sqrt{f}}=-2\log_{10}\biggr(\frac{\varepsilon}{3.7D}+\frac{2.51}{Re\sqrt{f}}\biggr);\,Transitional,\,Colebrook-White\,Eq,Re>4000\\~\\ \frac{1}{\sqrt{f}}=1.14-2\log_{10}\biggr(\frac{\varepsilon}{D}\biggr);\,Wholly \,Rough

𝑓 − Friction Factor
D – Inside Pipe Diameter[in]
𝜀 − Pipe Roughness[in]

F=\sqrt{\frac{1}{f}}

F=1fF=\sqrt{\frac{1}{f}}

𝐹 − Transmission Factor

Q=C_Q(\frac{T_b}{P_b})D^{2.5}F\biggr[ \frac{P_1^2-e^sP_2^2}{GT_fL_eZ} \biggr]^{0.5}

Q=CQ(TbPb)D2.5F[P12−esP22GTfLeZ]0.5Q=C_Q(\frac{T_b}{P_b})D^{2.5}F\biggr[ \frac{P_1^2-e^sP_2^2}{GT_fL_eZ} \biggr]^{0.5}

𝑄 − Flow Rate (FT3/day)
𝐶𝑄 − 38.774
𝑇𝑏 −Temperature Base (°R)
𝑃𝑏 − Pressure Base (psia)
𝑇𝑓 − Gas Flowing Temperature (°R)
𝐷 − Internal Diameter (in)
𝐹 − Transmission Factor
𝑘 − Pipe Roughness
𝑃1 − Upstream Pressure (psig)
𝑃2 − Downstream Pressure (psig)
𝐺 − Gas Specific Gravity
𝑍 − Compressibility Factor
Le − Pipe Segment Length including Expansion (mi)

s=\frac{C_S\triangle HG}{T_fZ}

s=CS△HGTfZs=\frac{C_S\triangle HG}{T_fZ}

𝑠 − Elevation adjustment parameter
𝐶𝑆 − 0.0375
𝑍 − Compressibility Factor
𝑇𝑓 − Gas Flowing Temperature (°R)
∆𝐻𝐺 − Change in Elevation (ft)

L_e=\frac{(e^s-1)}{s}

Le=(es−1)sL_e=\frac{(e^s-1)}{s}

𝐿𝑒 − Pipe Segment Length including Expansion (mi)
𝑠 − Elevation adjustment parameter

V=0.75\frac{Q_h}{D^2P_{avg}}

V=0.75QhD2PavgV=0.75\frac{Q_h}{D^2P_{avg}}

𝑉 − Velocity (ft/sec)
𝑄ℎ − Volumetric flow rate (scf/hr)
𝐷 − Internal Diameter (in)
𝑃𝑎𝑣𝑔 − Average Pipeline Pressure (psia)

For Small Pressure Drop P2 > 0.8 P1:

P_{avg}=\frac{(P_1-P_2)}{2}

Pavg=(P1−P2)2P_{avg}=\frac{(P_1-P_2)}{2}

For Large Pressure Drop:

P_{avg}=\frac{2}{3}\biggr[ P_1+P_2-\frac{P_1P_1}{P_1+P_2} \biggr]

Pavg=23[P1+P2−P1P1P1+P2]P_{avg}=\frac{2}{3}\biggr[ P_1+P_2-\frac{P_1P_1}{P_1+P_2} \biggr]

Case Guide

Part 1: Create Case

  1. Select the Colebrook-White application in the Hydraulics module.
  2. To create a new case, click the “Add Case” button.
  3. Enter Case Name, Location, Date and any necessary notes.
  4. Fill out all required parameters.
  5. Make sure the values you are inputting are in the correct units.
  6. Click the CALCULATE button to overview results

Input Parameters

  • Temperature base(°F)
  • Pressure base(psia)
  • Gas Flowing Temperature(°F)
  • Gas Specific Gravity
  • Compressibility Factor
  • Pipeline Efficiency Factor
  • Upstream Pressure(psig)
  • Downstream Pressure(psig)
  • Flow Rate(Barrels per Day)
  • Internal Pipe Diameter(in)
  • Length of Pipeline(mi)
  • Upstream Elevation(ft)
  • Downstream Elevation(ft)

Downstream Pressure

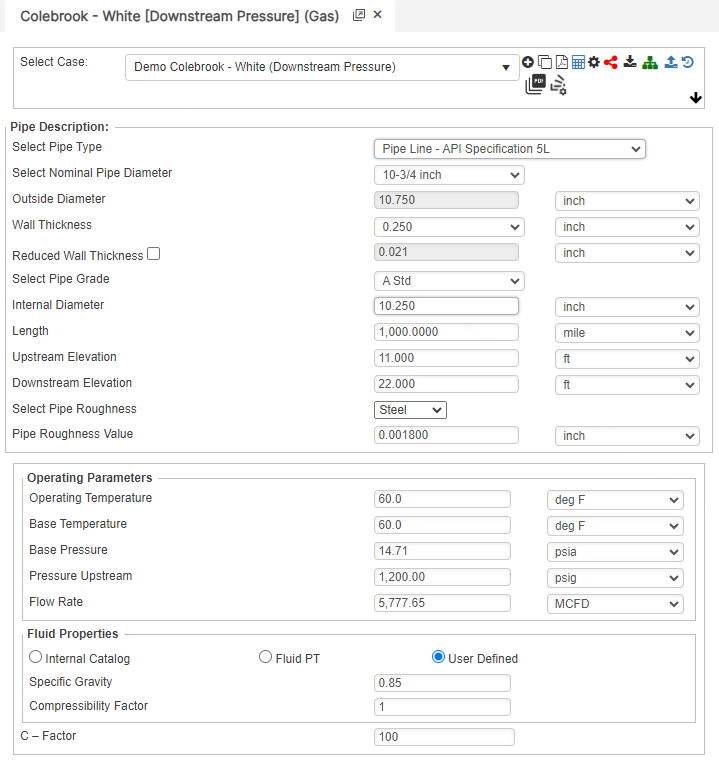
Flow Rate

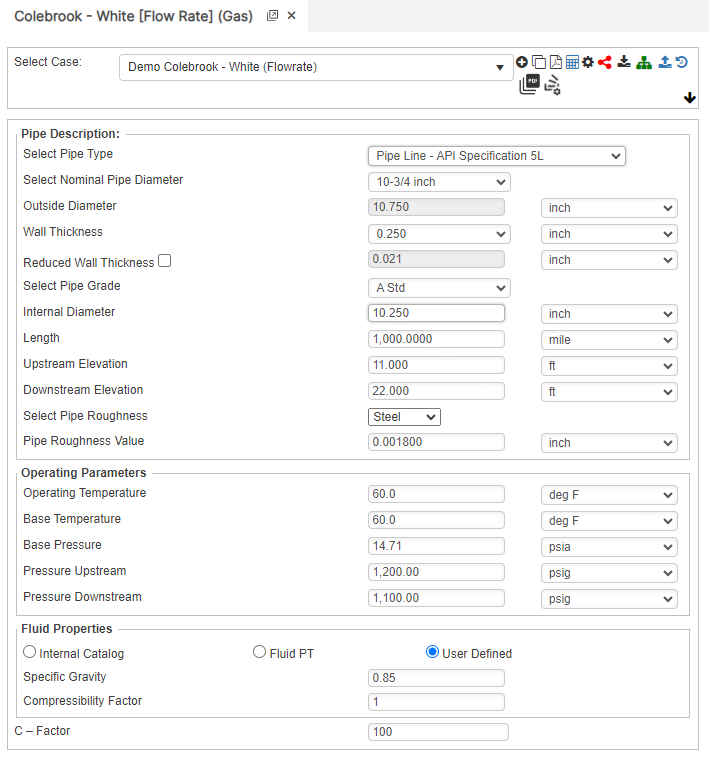
Internal Pipe Diameter

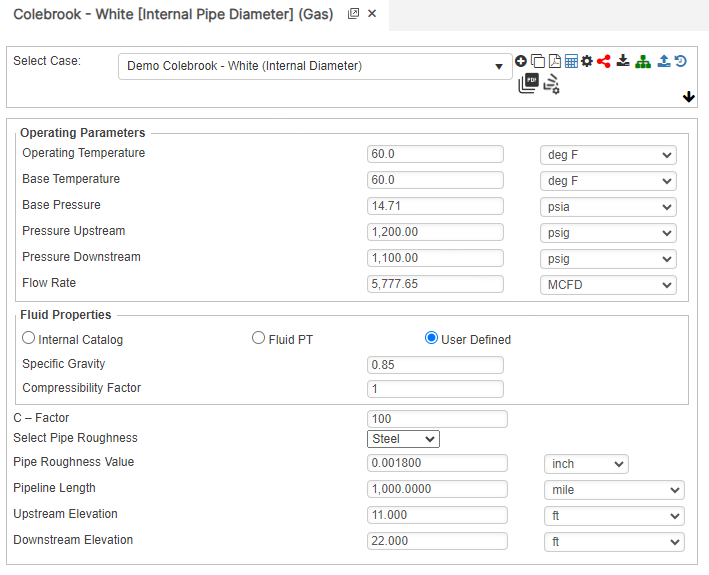
Upstream Pressure

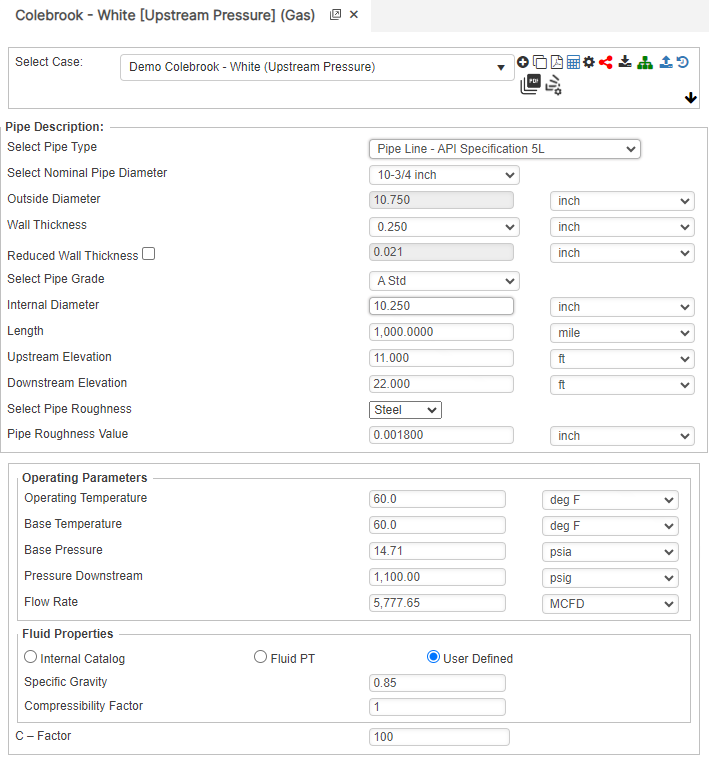
Part 2: Outputs/Reports

  1. If you need to modify an input parameter, click the CALCULATE button after the change.
  2. To SAVE, fill out all required case details then click the SAVE button.
  3. To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
  4. To generate a REPORT, click the REPORT button.
  5. The user may export the Case/Report by clicking the Export to Excel icon.
  6. To delete a case, click the DELETE icon near the top of the widget.

Results

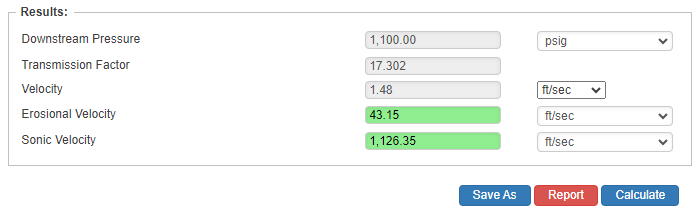
  • Downstream Pressure(psig)
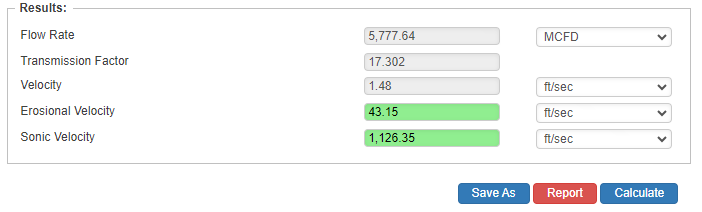
  • Flow Rate(ft/sec.)
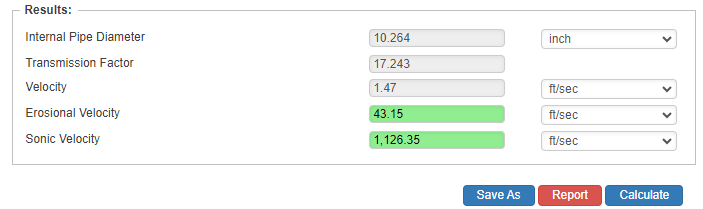
  • Internal Pipe Diameter(in)
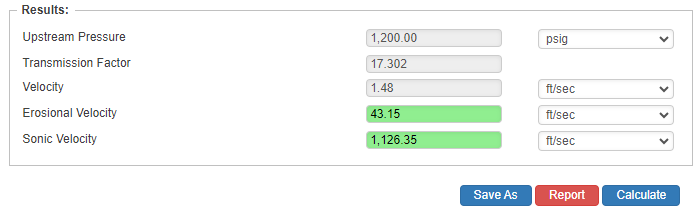
  • Upstream Pressure(psig)
  • Transmission Factor
  • Velocity(ft/sec.)
  • Erosional Velocity
  • Sonic Velocity

Downstream Pressure

Flow Rate

Internal Pipe Diameter

Upstream Pressure

References

  • “Pipeline Rules of Thumb” Gulf Professional Publishing, Seventh Edition, McAllister, E. W.
  • “Gas Pipeline Hydraulics”, Systek Technologies, Inc., Menon, Shahi E.
  • “Advanced Pipeline Design”, Carroll, Landon and Hudkins, Weston R.
  • American Gas Association (AGA), “Reference: Eq-17-18, Section 17, GPSA”, Engineering Data Book, Eleventh Edition
  • Hydraulic Transients, McGraw-Hill, New York., Streeter, V.L. and Wylie, E.B. (1967)
  • Water Hammer Analysis. Jour. Hyd. Div., ASCE., Vol. 88, HY3, pp79-113 May, Streeter, V.L. (1969)
  • Unsteady flow calculations by numerical methods’, Jour. Basic Eng., ASME., 94, pp457-466, June. Streeter, V.L. (1972),
  • Hydraulic Pipelines, John Wiley & Sons, J. P Tullis (1989)

FAQ

  • Gas Purging Calculations?

    Purging is a process of removing gas from the pipeline. Controlled purging of gases from pipelines by direct displacement with other gases that have been safely practiced for many years with the recognition that some flammable mixture is present. Purging of gases from pipelines by direct displacement with another gas also has been similarly practiced. It works both ways; however, there will always be an atmosphere of type of a mixture. This is due to the densities of the gases. Check Out

  • What is Erosional Velocity?

    Pipe erosion begins when velocity exceeds the value of C/SQRT(ρ) in ft/s, where ρ = gas density (in lb./ft3) and C = empirical constant (in lb./s/ft2) (starting erosional velocity). We used C=100 as API RP 14E (1984). However, this value can be changed based on the internal conditions of the pipeline. Check Out

  • What is Sonic Velocity?

    The maximum possible velocity of a compressible fluid in a pipe is called sonic velocity. Oilfield liquids are semi-compressible, due to dissolved gases. Check Out

Updated on December 19, 2023
Tagged:

Was this article helpful?

Yes No

Related Articles