Natural gas rupture includes three (3) models that determine depth, radius and Width of the crater. Gasunie, NEN 3651 Radius of Crater and PRCI/Gasunie/Battelle combined model.
GASUNIE MODEL
This model applies to a guillotine rupture wherein two separate pipe ends exists after the rupture.
Crater Depth:
𝑤 − Soil Parameter
𝐷𝑝 − Pipe Outside Diameter(m)
𝑝𝑜 − Pipe Pressure(Pa)
𝐷𝑐 − Depth of Cover from ground surface to center of the pipe(m)
𝐷 − Depth of Crater(m)
𝑅 − Soil Parameter Function


Soil Parameter Functions: R(w)=0.28+0.62(5-w)-0.07(25-w2)
R(w)=0.28+0.62(5-w)-0.07(25-w2)
Allowable limits for R are between 0.28 and 1.3:
if \,w\leq0.6 \;\;\;\;\;\;\;\;\;\; D=4.3D_p+D_c
if \,w\leq0.6 \;\;\;\;\;\;\;\;\;\; D=4.3D_p+D_c
if \,0.6< w<2 \;\;\;\;\;\;\;\;\;\; D=\frac {RD_p}{0.3}+D_c
if \,0.6< w<2 \;\;\;\;\;\;\;\;\;\; D=\frac {RD_p}{0.3}+D_cif \,w\geq2 \;\;\;\;\;\;\;\;\;\; D=2.2D_p+D_c
if \,w\geq2 \;\;\;\;\;\;\;\;\;\; D=2.2D_p+D_c
The crater angles are determined from empirical equations: \alpha_1 = tan^{−1}(𝑤 + 1)
\alpha_1 = tan^{−1}(𝑤 + 1)\alpha_2 = tan^{−1}[(\frac{2.8+0.5w}{10})(𝑤 + 1)]
\alpha_2 = tan^{−1}[(\frac{2.8+0.5w}{10})(𝑤 + 1)]Considering crater and dimensions shown in Figure 1. The equation of the ellipse is given by:
\frac {x^2}{a^2}+\frac {y^2}{b^2}=1
\frac {x^2}{a^2}+\frac {y^2}{b^2}=1Differentiating this at the ground level and substituting for x give: \frac {dx}{dy}=\frac{b}{a}\frac{{\sqrt {(b^2-y^2)}}}{y} \,For\,x>0
\frac {dx}{dy}=\frac{b}{a}\frac{{\sqrt {(b^2-y^2)}}}{y} \,For\,x>0Evaluating this on the ground level and half crater depth gives: tan\,\alpha_1=\frac{b}{a}\sqrt{{(\frac{b}{b-D}})^2-1}
tan\,\alpha_1=\frac{b}{a}\sqrt{{(\frac{b}{b-D}})^2-1}tan\,\alpha_2=\frac{b}{a}\sqrt{{(\frac{b}{b-0.5D}})^2-1}
tan\,\alpha_2=\frac{b}{a}\sqrt{{(\frac{b}{b-0.5D}})^2-1}These can be solved simultaneously: \frac {\frac{b}{a}\sqrt{{(\frac{b}{b-D}})^2-1}}{tan\,\alpha_1}=\frac {\frac{b}{a}\sqrt{{(\frac{b}{b-0.5D}})^2-1}}{tan\,\alpha_2}
\frac {\frac{b}{a}\sqrt{{(\frac{b}{b-D}})^2-1}}{tan\,\alpha_1}=\frac {\frac{b}{a}\sqrt{{(\frac{b}{b-0.5D}})^2-1}}{tan\,\alpha_2}The width of crater W is given by: W=2a\sqrt {1-\frac{(b-D)^2}{b^2}}
W=2a\sqrt {1-\frac{(b-D)^2}{b^2}}NEN 3651 MODEL RADIUS OF THE CRATER
Model may be applied for guillotine type rupture, NEN 3651 define radius of the crater as:
R_w=\sqrt{ 0.64(D_p^3p_o)^\frac{2}{3}+ 0.65(D_p^3p_o)^\frac{1}{3} -0.83D_c^2 }
R_w=\sqrt{ 0.64(D_p^3p_o)^\frac{2}{3}+ 0.65(D_p^3p_o)^\frac{1}{3} -0.83D_c^2 }PRCI/GASUNIE/BATTELLE COMBINED MODEL
This model may be applied for guillotine type rupture only. Computation of the crater depth in combined PRCI/Gasunie/Battelle model is the same as described above for Gasunie model.
The crater width is calculated as:
W= 2 \sqrt{ \frac{D_pW_w}{u_{kr}} \sqrt{ \frac{\gamma P_o}{3\rho_{𝑠𝑜𝑖𝑙}(\gamma^2-1)} }-W_w^{2} }\~\u_x= \sqrt{ \frac{\gamma P_o}{3\rho_{𝑠𝑜𝑖𝑙}(\gamma^2-1)}} \~\ W= 2 \sqrt{ \frac{D_pW_w}{u_{kr} }u_x-W_w^{2} }
W= 2 \sqrt{ \frac{D_pW_w}{u_{kr}} \sqrt{ \frac{\gamma P_o}{3\rho_{𝑠𝑜𝑖𝑙}(\gamma^2-1)} }-W_w^{2} }\\~\\u_x= \sqrt{ \frac{\gamma P_o}{3\rho_{𝑠𝑜𝑖𝑙}(\gamma^2-1)}} \\~\\ W= 2 \sqrt{ \frac{D_pW_w}{u_{kr} }u_x-W_w^{2} }Where:
RP= DP/2
𝑊𝑤 = 𝐷𝑐 + 𝑅𝑝 − Distance from the Ground to the Center of the Pipe[m]
𝜌𝑠𝑜𝑖𝑙 − Soil Density[kg/m3]
𝛾 − Gas Specific Heat Ratio(1.031 for Natural Gas)
𝑢𝑘𝑟 = 2.54[m/s] − Critical Gas Velocity [m/s]
𝑢𝑥 − Velocity of the Explosive Gases[m/s]
Case Guide
Part 1: Create Case
- Select the Natural Gas Pipeline Rupture – Width, Radius, Depth of Crater application in the AGR & GPRA module.
- To create a new case, click the “Add Case” button.
- Enter Case Name, Location, Date and any necessary notes.
- Fill out all required parameters.
- Make sure the values you are inputting are in the correct units.
- Click the CALCULATE button to overview results.
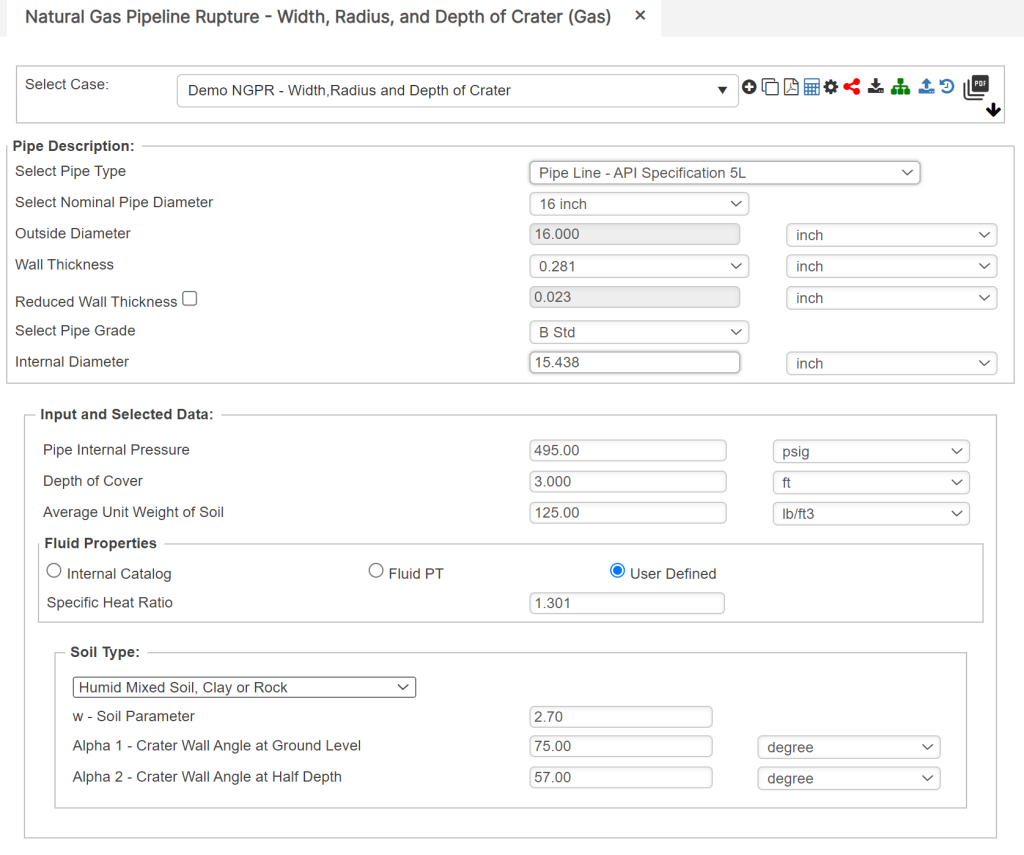
Input Parameters
- Pipe Outside Diameter
- Pipe Internal Pressure
- Depth of Cover
- Average Unit Weight of Soil
- Natural Gas Specific Heat Ratio
- Soil Type
- w – Soil Parameter
- Alpha 1 – Crater Wall Angle at Ground Level
- Alpha 2 – Crater Wall Angle at Half Depth
Part 2: Outputs/Reports
- If you need to modify an input parameter, click the CALCULATE button after the change.
- To SAVE, fill out all required case details then click the SAVE button.
- To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
- To generate a REPORT, click the REPORT button.
- The user may export the Case/Report by clicking the Export to Excel icon.
- To delete a case, click the DELETE icon near the top of the widget.
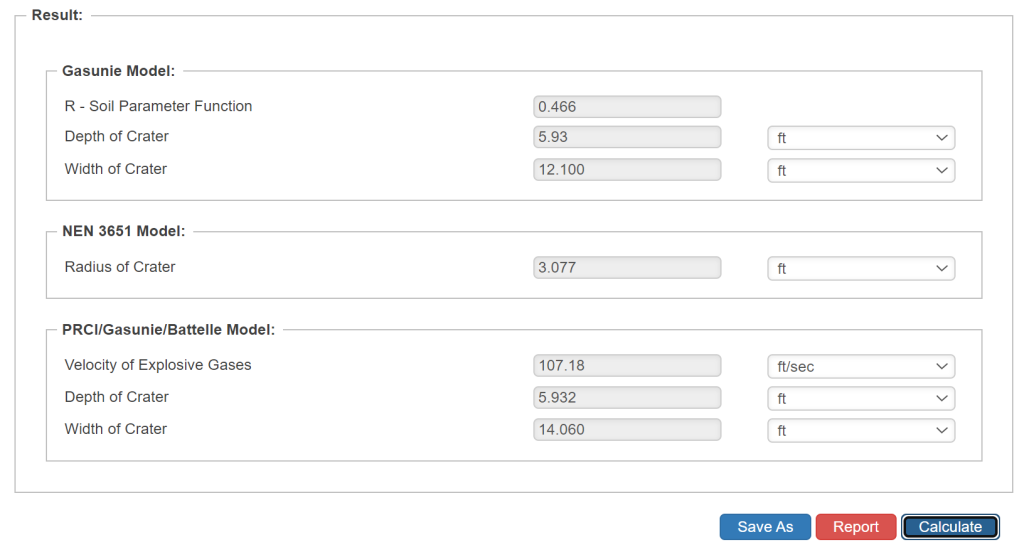
Results
- Gasunie Model
- R – Soil Parameter Function
- Depth of Crater
- Width of Crater
- NEN 3651 Model
- Radius of Crater
- PRCI/Gasunie/Battelle Model
- Velocity of Explosive Gases
- Depth of Crater
- Width of Crater
References
- GRI-00/0189, A Model for Sizing High Consequence Areas Associated with Natural Gas Pipelines, Gas Technology Institute
- PHMSA – Final Report TTO Number 13, Delivery Order DTRS56-02-D-70036, Michael Baker Jr., Inc. –
- PHMSA – Final Report TTO Number 14, Delivery Order DTRS56-02-D-70036, , Michael Baker Jr., Inc.
- Crane Limited, Flow of Fluids through Valves, Fittings, and Pipe, Technical Paper No. 410-C, Crane Engineering Division
- Schram, W., “Prediction of Crater Caused by Underground Pipeline Rupture”, N.V. Nederland se Gasunie, Report TR/T 97.R.2515
- NEN 3651, Annex A: “Determining Disturbance Zone Dimension”
- PRCI L51861, “Line Rupture and Spacing of Parallel Lines”, Battelle Memorial Institute
