Overview of Sleeve End Fillet Weld SIF Equations

The following section presents an overview of the SIF equations that were developed as part of the previous PRCI project.

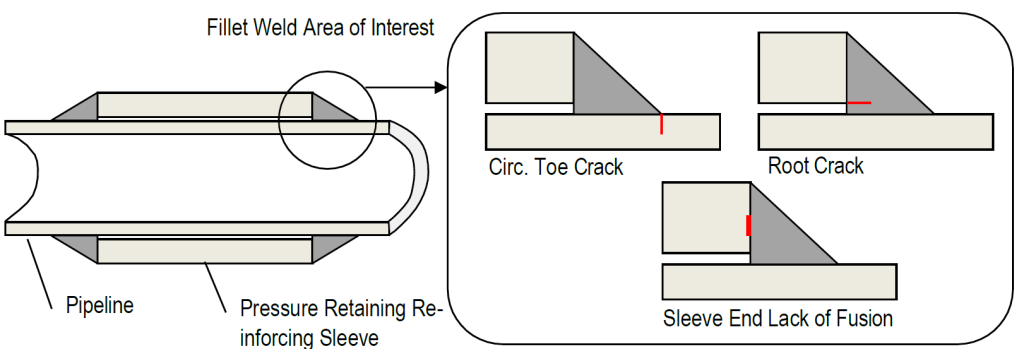
Sleeve End Fillet Weld Cracking Scenarios

SIF equations were developed for the following three potential circumferential crack locations (illustrated in Figure 2.1):

1. Cracking through the carrier pipe at the toe of the fillet weld.
2. Cracking in the weld root, through the throat of the fillet weld.
3. Cracking through the sleeve end weld face, representative of lack of fusion (LOF) features at the sleeve end face.

For each location the cracks were assumed to be idealized semi-elliptical surface breaking planar flaws.

For each location, SIFs were developed for both the deepest point and the surface breaking points along the crack front for the following three loading scenarios:

• Internal pressure in the carrier pipe only.
• Internal pressure in both the carrier pipe and the annulus between the carrier pipe and the sleeve (simulating either through cracked carrier pipe or a carrier pipe that has been tapped).
• Axial tension on the carrier pipe.

SIF Equation Format

The mode I stress intensity factor (SIF or K) for a semi-elliptical surface flaw, shown in Figure 2.2, can be expressed using the following equation:

K=M\sigma\sqrt{\frac{\pi a}{Q}}

K=M\sigma\sqrt{\frac{\pi a}{Q}}

Where:

σ = applied nominal stress
a = flaw depth
Q = flaw shape parameter
M = geometry factor (normalized stress intensity factor)

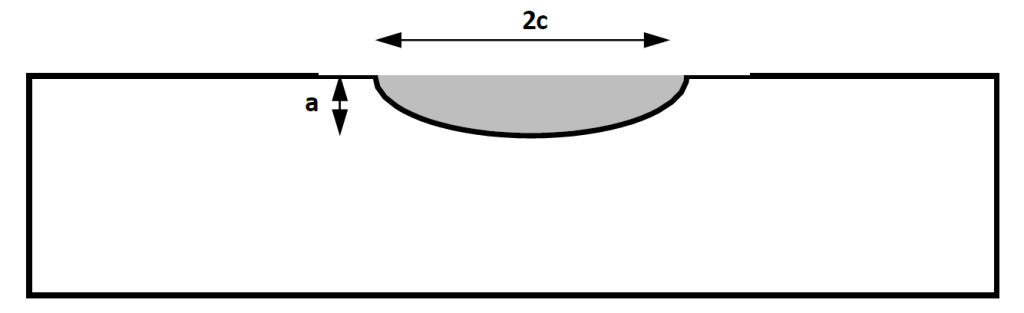
The flaw shape factor (Q) is given by the following equation, based on the half flaw length (c) and the flaw depth (a).

Q=1+1.454\left(\frac{a}{c} \right)^{1.65}

Q=1+1.454\left(\frac{a}{c} \right)^{1.65}

The SIF equations developed in the original project were developed in terms of normalized stress intensity factors M:

M = \frac{K}{\left( \Delta P;\sigma_{\text{axial}} \right) \sqrt{\frac{\pi a}{Q}}}

M = \frac{K}{\left( \Delta P;\sigma_{\text{axial}} \right) \sqrt{\frac{\pi a}{Q}}}

Note: that depending on the loading scenario being evaluated the nominal applied stress is taken to be either ΔP (for pressure in the carrier pipe only or pressure in both the pipe and annulus) or the axial tensile stress on the carrier pipe (σ_axial for the axial tension case). ΔP used in the calculation of M is the difference between the internal pressure at the time of the sleeve installation and the pressure being evaluated.

The regression equations developed relate the normalized stress intensity factor (M) to the five basic non- dimensional geometric parameters used to define a pipe-sleeve scenario, summarized below: 

1. The crack depth ratio, (a/tp). considering crack depth (a) and pipe thickness (tp) 
2. The crack aspect ratio, (c/a). Considering half crack length (c) and depth (a). 
3. The ratio of the pipe outer diameter (OD) to the pipe wall thickness (OD/tp). 
4. The ratio of the sleeve wall thickness (ts) to the pipe wall thickness (ts/tp). 
5. The ratio of the sleeve length (L) to the pipe outer diameter (L/OD). 

The equations used to calculate the normalized stress intensity factor (M) consist of a series of nested polynomial equations, relating the coefficients to one of the five geometry ratios. Different equation formats were developed for each location and loading combination. An example set of equations for a circumferential surface flaw in a weld toe for internal pressure in the carrier pipe only are summarized below: 

M = A_{1} \left( \frac{a}{t_{p}} \right)^2 + A_{2} \left( \frac{a}{t_{p}} \right) + A_{3}\~\A_{i} = B_{i,1} \left( \frac{c}{a} \right)^2 + B_{i,2} \left( \frac{c}{a} \right) + B_{i,3}\~\B_{i,j} = C_{i,j,1} \left( \frac{OD}{t_{p}} \right) + C_{i,j,2}\~\C_{i,j,k} = D_{i,j,k,1} \left( \frac{t_{s}}{t_{p}} \right)^2 + D_{i,j,k,2} \left( \frac{t_{s}}{t_{p}} \right) + D_{i,j,k,3}

M = A_{1} \left( \frac{a}{t_{p}} \right)^2 + A_{2} \left( \frac{a}{t_{p}} \right) + A_{3}\\~\\A_{i} = B_{i,1} \left( \frac{c}{a} \right)^2 + B_{i,2} \left( \frac{c}{a} \right) + B_{i,3}\\~\\B_{i,j} = C_{i,j,1} \left( \frac{OD}{t_{p}} \right) + C_{i,j,2}\\~\\C_{i,j,k} = D_{i,j,k,1} \left( \frac{t_{s}}{t_{p}} \right)^2 + D_{i,j,k,2} \left( \frac{t_{s}}{t_{p}} \right) + D_{i,j,k,3}

The software developed as part of this project automates the calculation of the normalized stress intensity factor (M) and the actual stress intensity factor (K), for all three crack locations and all three loading conditions based on user defined inputs. 

References

• In the Matter of an Accident on 19 February 1985 near Camrose, Alberta on the Pipeline System of Interprovincial Pipe Line ”, National Energy Board, Canada, 1986.
• F. Cross and C.A. Robertson, “Northeast U.S. products line upgraded after major line break”, Oil and Gas Journal, February 15 1988, Vol. 86, No. 7, pp 35 40.
• “Development of Sleeve End Fillet Weld Fitness for Service Assessment Tools”, PRCI Contract Num- ber PR-214-114504, April 22, 2016.
• API 579-2/ASME FFS-1 “Fitness-for-Service, American Petroleum Institute and the American Soci- ety of Mechanical Engineers, June 2007.

FAQ