Panhandle B

Introduction

Panhandle B equation is used in the design of large high pressure, long transmission pipelines.

The Panhandle B equation is considered suitable for Reynolds numbers from: R_e=4\times10^6\,to\,40\times11^6

R_e=4\times10^6\,to\,40\times11^6

The equation can be adjusted through the use of an efficiency term that makes it applicable across a relatively limited range of Reynolds numbers. Other than this, however, there are no means for adjustment of the equation to correct it for variations in pipe surface. Adjusted to an average flowing Reynolds number, the equation will predict low flow rates at low Reynolds numbers, and high flow rates at high Reynolds numbers, as compared to a fully turbulent flow equation. Efficiencies based on the Panhandle B equation decrease with increasing flow rate for fully turbulent flow. The efficiency factor, E, used in the Panhandle B equation generally varies between about 0.88 and 0.94.

These Panhandle A and B equations suffer from the substitution of a fixed gas viscosity value into the Reynolds number expression, which, in turn, substituted into the flow equation, results in an expression with a preconditioned bias. : F=EC_F(\frac{QG}{D})^{0.01961}

F=EC_F(\frac{QG}{D})^{0.01961}

𝐹 − Transmission Factor
E – Pipeline Efficiency Factor
𝐶_𝑓 − 16.7
𝑄 − Flow Rate (FT³/day)
𝐺 − Gas Specific Gravity
𝐷 − Internal Diameter (in)

Q=EC_Q(\frac{T_b}{P_b})^{1.02}D^{2.53}\biggr[ \frac{P_1^2-e^sP_2^2}{G^{0.961}T_fL_e} \biggr]^{0.51}

Q=EC_Q(\frac{T_b}{P_b})^{1.02}D^{2.53}\biggr[    \frac{P_1^2-e^sP_2^2}{G^{0.961}T_fL_e}    \biggr]^{0.51}

𝑄 − Flow Rate (FT³/day)
E – Pipeline Efficiency Factor
𝐶_𝑄 − 737
𝑇_𝑏 − Temperature Base (°R)
𝑃_𝑏 − Pressure Base (psia)
𝐷 − Internal Diameter (in)
𝑃₁ − Upstream Pressure (psig)
𝑃₂ − Downstream Pressure (psig)
𝐺 − Gas Specific Gravity
𝐿_𝑒 − Pipe Segment Length including Expansion (mi)
𝑇_𝑓 − Gas Flowing Temperature(°R)

s=\frac{C_S\triangle HG}{T_fZ}

s=\frac{C_S\triangle HG}{T_fZ}

𝑠 − Elevation adjustment parameter
𝐶_𝑆 − 0.0375
𝑍 − Compressibility Factor
𝑇_𝑓 − Gas Flowing Temperature(°R)
∆𝐻𝐺 − Change in Elevation(ft)

L_e=\frac{(e^s-1)}{s}

L_e=\frac{(e^s-1)}{s}

𝐿_𝑒 − Pipe Segment Length including Expansion(mi)
𝑠 − Elevation adjustment parameter

V=0.75\frac{Q_h}{D^2P_{avg}}

V=0.75\frac{Q_h}{D^2P_{avg}}

𝑉 − Velocity (ft/sec)
𝑄_ℎ − Volumetric flow rate (scf/hr)
𝐷 − Internal Diameter (in)
𝑃_𝑎𝑣𝑔 − Average Pipeline Pressure (psia)

For Small Pressure Drop P2 > 0.8 P1:

P_{avg}=\frac{(P_1-P_2)}{2}

P_{avg}=\frac{(P_1-P_2)}{2}

For Large Pressure Drop:

P_{avg}=\frac{2}{3}\biggr[ P_1+P_2-\frac{P_1P_1}{P_1+P_2} \biggr]

P_{avg}=\frac{2}{3}\biggr[  P_1+P_2-\frac{P_1P_1}{P_1+P_2}    \biggr]

Case Guide

Part 1: Create Case

Input Parameters

• Temperature base(°F)
• Pressure base(psia)
• Gas Flowing Temperature(°F)
• Gas Specific Gravity
• Compressibility Factor
• Pipeline Efficiency Factor
• Upstream Pressure(psig)
• Downstream Pressure(psig)
• Flow Rate(MCFD)
• Internal Pipe Diameter(in)
• Length of Pipeline(mi)
• Upstream Elevation(ft)
• Downstream Elevation(ft)

Downstream Pressure

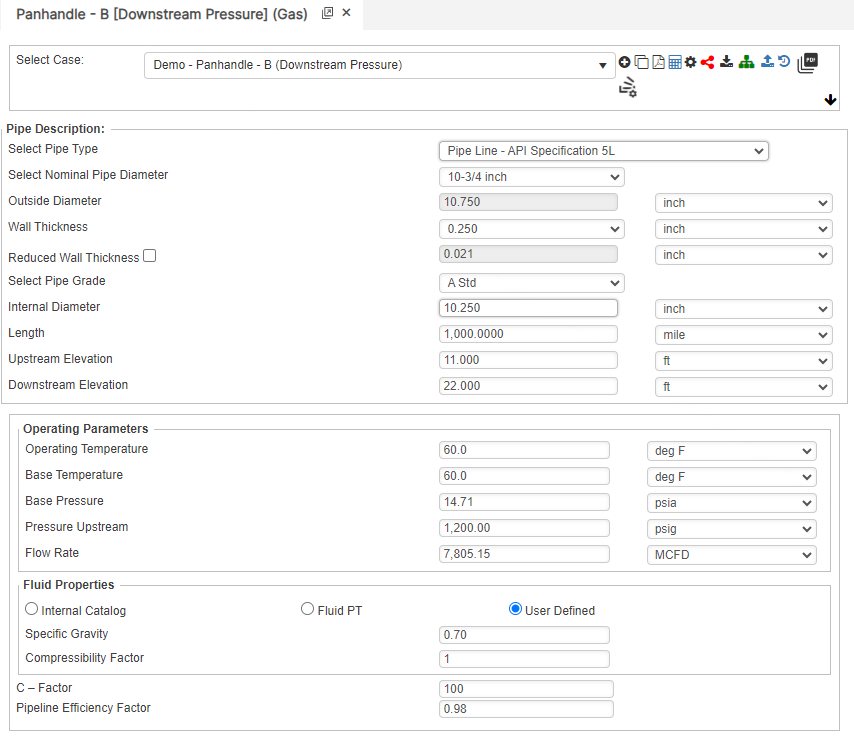
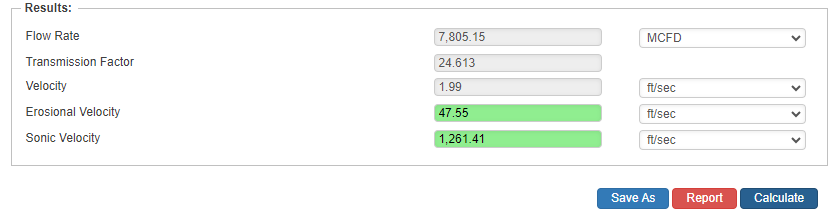
Flow Rate

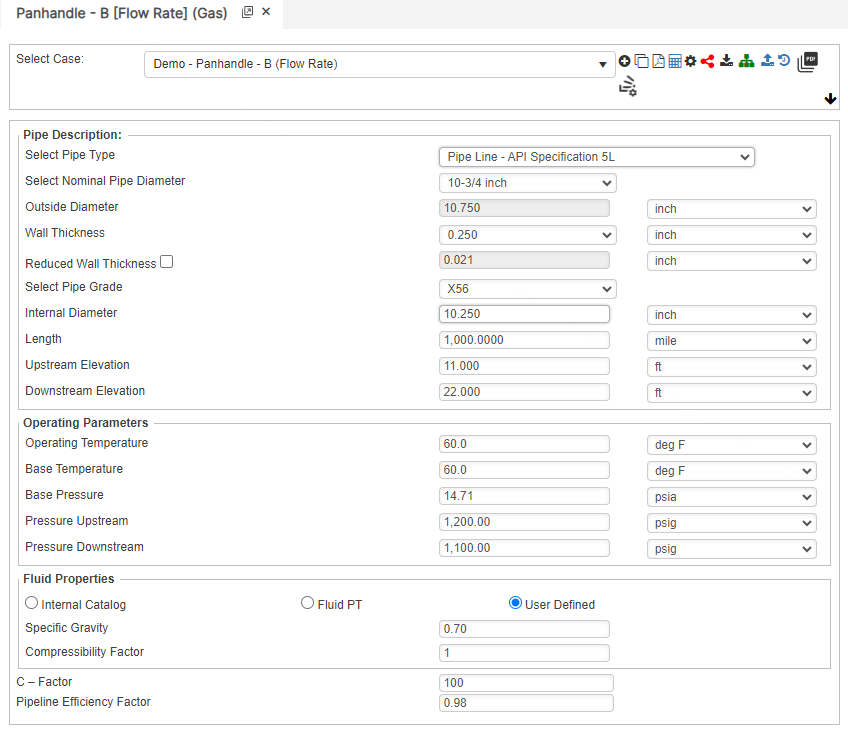
Internal Pipe Diameter

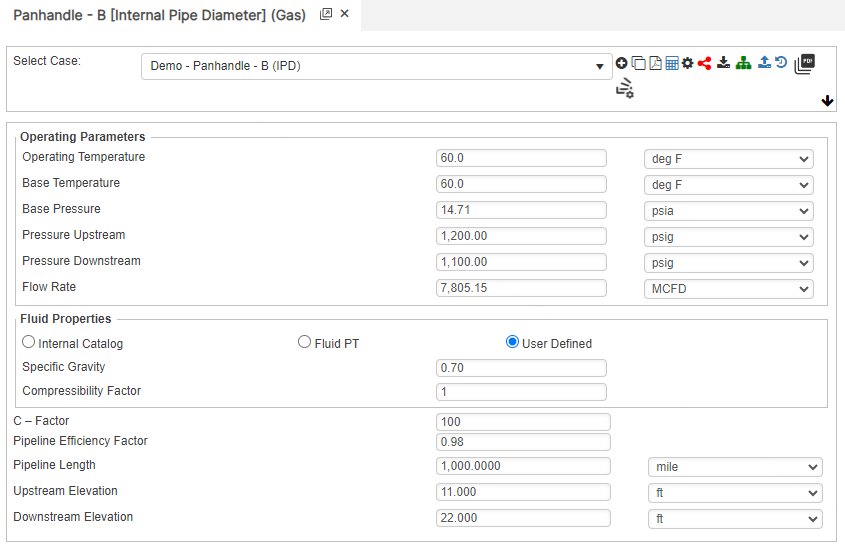
Upstream Pressure

Part 2: Outputs/Reports

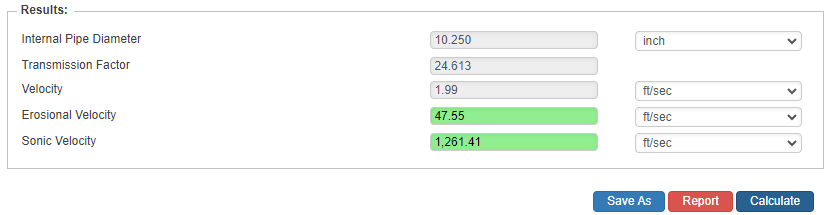
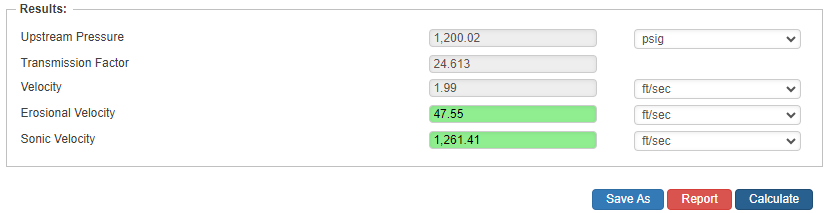
Results

• Downstream Pressure(psig)
• Flow Rate(ft/sec.)
• Internal Pipe Diameter(in)
• Upstream Pressure(psig)
• Transmission Factor
• Velocity(ft/sec.)
• Erosional Velocity
• Sonic Velocity

Downstream Pressure

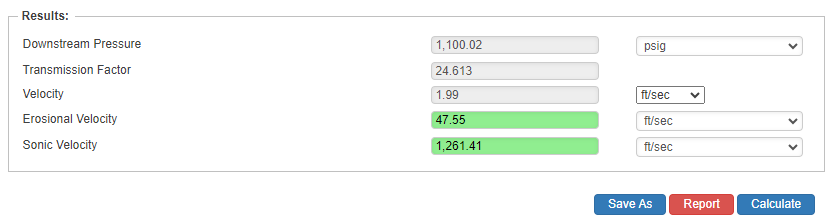
Flow Rate

Internal Pipe Diameter

Upstream Pressure

References

• McAllister, E. W., “Pipeline Rules of Thumb” Gulf Professional Publishing, Seventh Edition
• Menon, Shahi E., “Gas Pipeline Hydraulics”, Systek Technologies, Inc.
• Carroll, Landon and Hudkins, Weston R., “Advanced Pipeline Design”
• American Gas Association (AGA), “Reference: Eq-17-18, Section 17, GPSA”, Engineering Data Book, Eleventh Edition

FAQ