PE Pipe Pull Force and Installation Stresses

Pull Force and Installation Stresses

The procedures for designing the bore path for plastic pipe are basically the same as discussed for steel pipe. As with steel product pipe, plastic pipe, when installed by HDD, may experience high-tension loads, severe bending, and external fluid pressures. HDD installation subjects the pipe to axial tensile forces caused by the frictional drag between the pipe and the borehole or drilling fluid, the frictional drag on the ground surface, the capstan effect around drill-path bends, and hydrokinetic drag. The pipe may also be subjected to external hoop pressures caused by the external fluid head and bending stresses. Estimating of pullback forces involves the assumption of many variables and installation techniques.

Calculation Overview

Estimated average radius of curvature at pipe entry and pipe exit:

R_{avgin}=\frac{H_1}{\theta_{in}^2}\~\R_{avgex}=\frac{H_2}{\theta_{ex}^2}

R_{avgin}=\frac{H_1}{\theta_{in}^2}\\~\\R_{avgex}=\frac{H_2}{\theta_{ex}^2}

H1, H2 – Depth of bore (ft)
Θ_in – Pipe entry angle (degree)
Θ_ex – Pipe exit angle (degree)

L₂ – Horizontal Distance to Achieve Desired Depth:

L_2=\frac{H_1}{\theta_{in}^2}

L_2=\frac{H_1}{\theta_{in}}

L₄ – Horizontal Distance to Achieve Rise to the Surface:

L_4=\frac{H_2}{\theta_{ex}^2}

L_4=\frac{H_2}{\theta_{ex}}

L₃ – Additional Distance Traversed at Desired Depth:

L_3=L_{cross}-L_2-L_4

L_3=L_{cross}-L_2-L_4

L_cross – Length of the Crossing

Weight of Empty Pipe:

pipe_{weight} = \pi D^2 \left( \frac{DR – 1}{DR^2} \right) \rho_w\cdot \gamma_a

pipe_{weight} = \pi D^2 \left( \frac{DR - 1}{DR^2} \right) \rho_w\cdot \gamma_a

D – Pipe Diameter (inch)
DR – Pipe Dimension Ratio
ρ_w – Density of Water (lbf/inch3)
γ_a – Specific Gravity of Pipe Material

Average Weight of Empty Pipe:

w_a=1.06\,pipe_{weight}

w_a=1.06\,pipe_{weight}

Net Upward Buoyant Force on Empty Pipe:

w_b = \pi \cdot \frac{D^2}{4} \cdot \rho_w \gamma_b – w_a

w_b = \pi \cdot \frac{D^2}{4} \cdot \rho_w \gamma_b - w_a

γ_b – Specific Gravity of the mud slurry

Hydrokinetic Force:

D_{bh} = 1.5D\~\T_{hk} = hydro_{pressure} \cdot \frac{\pi}{8} (D_{bh}^2 – D^2)

D_{bh} = 1.5D\\~\\T_{hk} = hydro_{pressure} \cdot \frac{\pi}{8} (D_{bh}^2 - D^2)

Pull Force at point A:

T_1 = \exp(v_a \theta_{\text{in}}) \cdot [v_a \cdot w_a (L_1 + L_2 + L_3 + L_4)]

T_1 = \exp(v_a \theta_{\text{in}}) \cdot [v_a \cdot w_a (L_1 + L_2 + L_3 + L_4)]

Pull Force at point B:

T_2 = \exp(v_{a} \theta_{in}) \cdot [T_1 + T_{hk} + v_b \cdot |w_b| \cdot L_2 + w_b \cdot H – v_a \cdot w_a L= \exp(v_a\theta_{in})]

T_2 = \exp(v_{b} \theta_{in}) \cdot [T_1 + T_{hk} + v_b \cdot |w_b| \cdot L_2 + w_b \cdot H_1 - v_a \cdot w_a L_2 \exp(v_a\theta_{in})]

Pull Force at point C:

T_3 = [T_2 + v_b \cdot |w_b| \cdot L_3 – \exp (v_{a} \cdot \theta_{in})\cdot{v_a w_a L_3 \exp(v_a \theta_{\text{in}})}]

T_3 = [T_2  + v_b \cdot |w_b| \cdot L_3 - \exp (v_{b} \cdot \theta_{in})\cdot\{v_a w_a L_3 \exp(v_a \theta_{\text{in}})\}]

Pull Force at point D:

T_4 = \exp(v_b \theta_{\text{ex}}) [T_3 + v_b \cdot |w_b| \cdot L_4 – w_b \cdot H – \exp(v_b \theta_{\text{in}}) \cdot {v_a w_a L_4 \exp(v_a \theta_{\text{in}})}]

T_4 = \exp(v_b \theta_{\text{ex}}) \cdot  [T_3 + v_b \cdot |w_b| \cdot L_4 - w_b \cdot H_2 - \exp(v_b \theta_{\text{in}}) \cdot \{v_a w_a L_4 \exp(v_b \theta_{\text{in}})\}]

ν_a – Coefficient of Friction between Pipe and Soil (typically 0.4)
ν_b – Coefficient between Pipe and Slurry (typically 0.25)

Bending Strain:

\varepsilon_{\text{ain}} = \frac{D}{2 \cdot R_{\text{avgin}}}\~\\varepsilon_{\text{aex}} = \frac{D}{2 \cdot R_{\text{avgex}}}

\varepsilon_{\text{ain}} = \frac{D}{2 \cdot R_{\text{avgin}}}\\~\\\varepsilon_{\text{aex}} = \frac{D}{2 \cdot R_{\text{avgex}}}

Bending Stress:

\delta_{\text{ain}} = E_{24} \cdot \varepsilon_{\text{ain}}\~\\delta_{\text{aex}} = E_{24} \cdot \varepsilon_{\text{aex}}

\delta_{\text{ain}} = E_{short} \cdot \varepsilon_{\text{ain}}\\~\\\delta_{\text{aex}} = E_{short} \cdot \varepsilon_{\text{aex}}

E_short  = Pullback Modulus of Elasticity (typically short-term or 10 hr)

Allowable Tensile Stress:

\delta_{\text{allow}} = \delta_{sp}-\frac{E_{24}\cdot D}{2\cdot R_{avgex}}

\delta_{\text{allow}} = \delta_{sp}-\frac{E_{short}\cdot D}{2\cdot R_{avgex}}

δ_sp – Allowable/Safe Pull Stress (psi)

Tensile Stress at Point A:

\sigma_1 = \frac{T_1}{\pi \cdot D^2} \left( \frac{DR^2}{DR – 1} \right)\~\\frac{\text{PASS}}{\text{FAIL}} =
\begin{cases}
\text{PASS if } \sigma_1 < \delta_{\text{allow}} \ \text{FAIL if } \sigma_1 > \delta_{\text{allow}}
\end{cases}

\sigma_1 = \frac{T_1}{\pi \cdot D^2} \left( \frac{DR^2}{DR - 1} \right)\\~\\\frac{\text{PASS}}{\text{FAIL}} =
\begin{cases}
\text{PASS if } \sigma_1 < \delta_{\text{allow}} \\
\text{FAIL if } \sigma_1 > \delta_{\text{allow}}
\end{cases}

Tensile Stress at Point B:

\sigma_2 = \frac{T_2}{\pi \cdot D^2} \left( \frac{DR^2}{DR – 1} \right) + \frac{E_{24} \cdot D}{2 \cdot R_{\text{avgin}}} + \delta_{\text{ain}}

\sigma_2 = \frac{T_2}{\pi \cdot D^2} \left( \frac{DR^2}{DR - 1} \right) + \frac{E_{short} \cdot D}{2 \cdot R_{\text{avgin}}} + \delta_{\text{ain}}

Tensile Stress at Point C:

\sigma_3 = \frac{T_3}{\pi \cdot D^2} \left( \frac{DR^2}{DR – 1} \right)

\sigma_3 = \frac{T_3}{\pi \cdot D^2} \left( \frac{DR^2}{DR - 1} \right)

Tensile Stress at Point D:

\sigma_4 = \frac{T_4}{\pi \cdot D^2} \left( \frac{DR^2}{DR – 1} \right) + \frac{E_{24} \cdot D}{2 \cdot R_{\text{avgex}}} + \delta_{\text{aex}}

\sigma_4 = \frac{T_4}{\pi \cdot D^2} \left( \frac{DR^2}{DR - 1} \right) + \frac{E_{short} \cdot D}{2 \cdot R_{\text{avgex}}} + \delta_{\text{aex}}

Breakaway Links Settings:

F_b = \delta_{sp} \cdot \frac{\pi}{4} \cdot (D^2 – ID^2)\~\\text{Result}{\text{pull}} = \begin{cases} \text{PASS if Total}{\text{pull}} < F_b \ \text{FAIL if Total}_{\text{pull}} > F_b
\end{cases}

F_b = \delta_{sp} \cdot \frac{\pi}{4} \cdot (D^2 - ID^2)\\~\\\text{Result}_{\text{pull}} =
\begin{cases}
\text{PASS if Total}_{\text{pull}} < F_b \\
\text{FAIL if Total}_{\text{pull}} > F_b
\end{cases}

Static Head Pressure:

P_{ext} = \rho_w \cdot \gamma_b \cdot H

P_{ext} = \rho_w \cdot \gamma_b \cdot H

H = depth of the bore profile (ft), usually the depth of the horizontal section

γ_b – Specific Gravity of the mud slurry

𝜌_𝑤 = Density of water (lb/ft3)

Maximum Pressure During Pullback:

P_{max} = P_{ext} + hydro_{pressure}

P_{max} = P_{ext} + hydro_{pressure}

Ovality Compensation Factor:

\%\Delta D = \frac{0.0125 P_{max}}{\frac{E_{long}}{12(DR – 1)^3}}\cdot100

\%\Delta D = \frac{0.0125 P_{max}}{\frac{E_{short}}{12(DR - 1)^3}}\cdot100

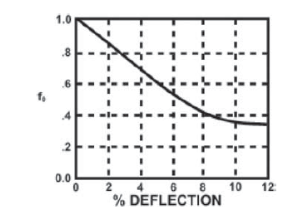
f₀ – Ovality compensation factor based on % of Deflection (%Δ𝐷)

Tensile Reduction Factor:

r = \frac{\sigma_4}{2 \cdot \delta_{\text{allow}}}\~\f_r = \left(\sqrt{\left(5.57 – (r + 1.09)\right)^2} \right)- 1.09

r = \frac{\sigma_4}{2 \cdot \delta_{\text{allow}}}\\~\\f_r = \left(\sqrt{\left(5.57 - (r + 1.09)\right)^2} \right)- 1.09

Critical Collapse Pressure:

Pcr = \frac{2E_{24}}{1 – \mu^2} \left( \frac{1}{DR – 1} \right)^3 \cdot f_o\cdot f_r

Pcr = \frac{2E_{short}}{1 - \mu^2} \left( \frac{1}{DR - 1} \right)^3 \cdot f_o\cdot f_r

Safety Factor:

SF=\frac{P_{cr}}{P_{max}}

SF=\frac{P_{cr}}{P_{max}}

Input Parameters

Pipe Properties:

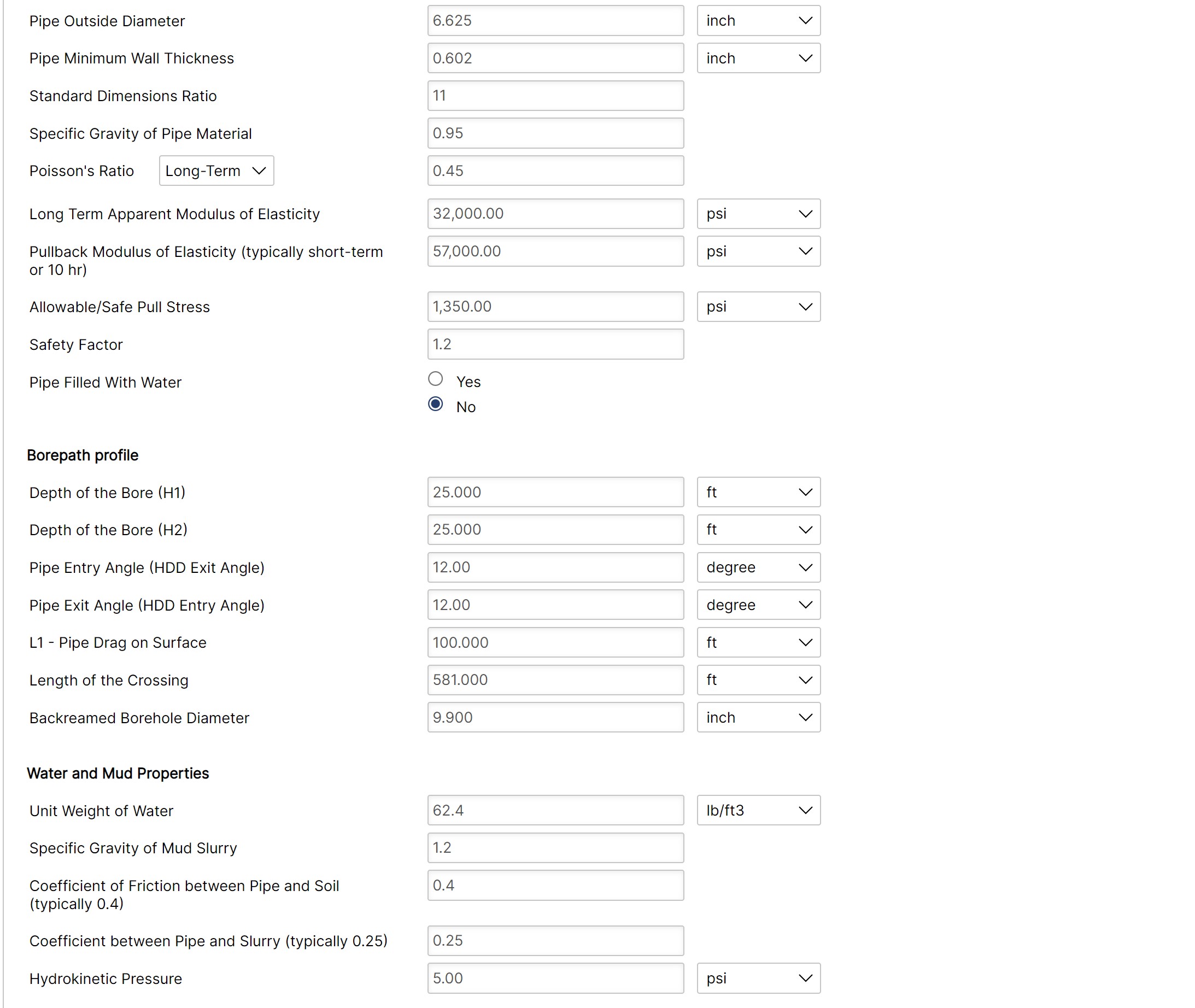
• Pipe Outside Diameter (in)
• Pipe Minimum Wall Thickness (in)
• Standard Dimensions Ratio
• Specific Gravity of Pipe Material
• Poisson’s Ratio
• Long Term Apparent Modulus of Elasticity (psi)
• Pullback Modulus of Elasticity (typically short-term or 10 hr)
• Allowable/Safe Pull Stress (psi)
• Safety Factor

Borehole Path:

• Depth of the Bore [H1] (ft)
• Depth of the Bore [H2] (ft)
• Pipe Entry Angle (HDD Exit Angle) (degree)
• Pipe Exit Angle (HDD Entry Angle) (degree)
• L₁ – Pipe Drag on Surface (ft)
• Length of the Crossing (ft)
• Backreamed Borehole Diameter (inch)

Water and Mud Properties:

• Unit Weight of Water (lb/ft³⁾
• Specific Gravity of Mud Slurry
• Coefficient of Friction between Pipe and Soil (typically 0.4)
• Coefficient between Pipe and Slurry (typically 0.25)
• Hydrokinetic Pressure (psi)

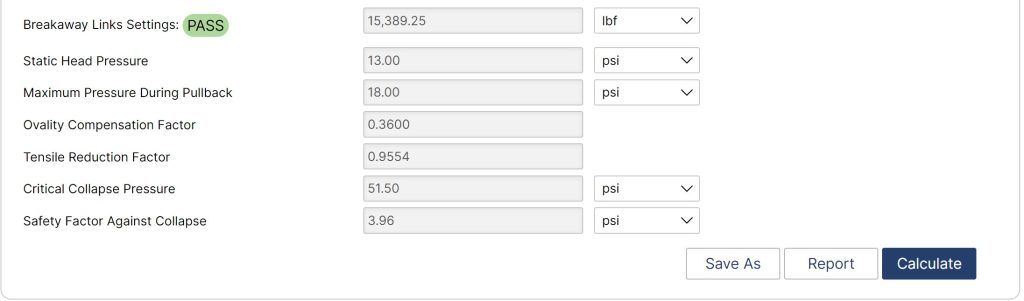
Outputs/Reports

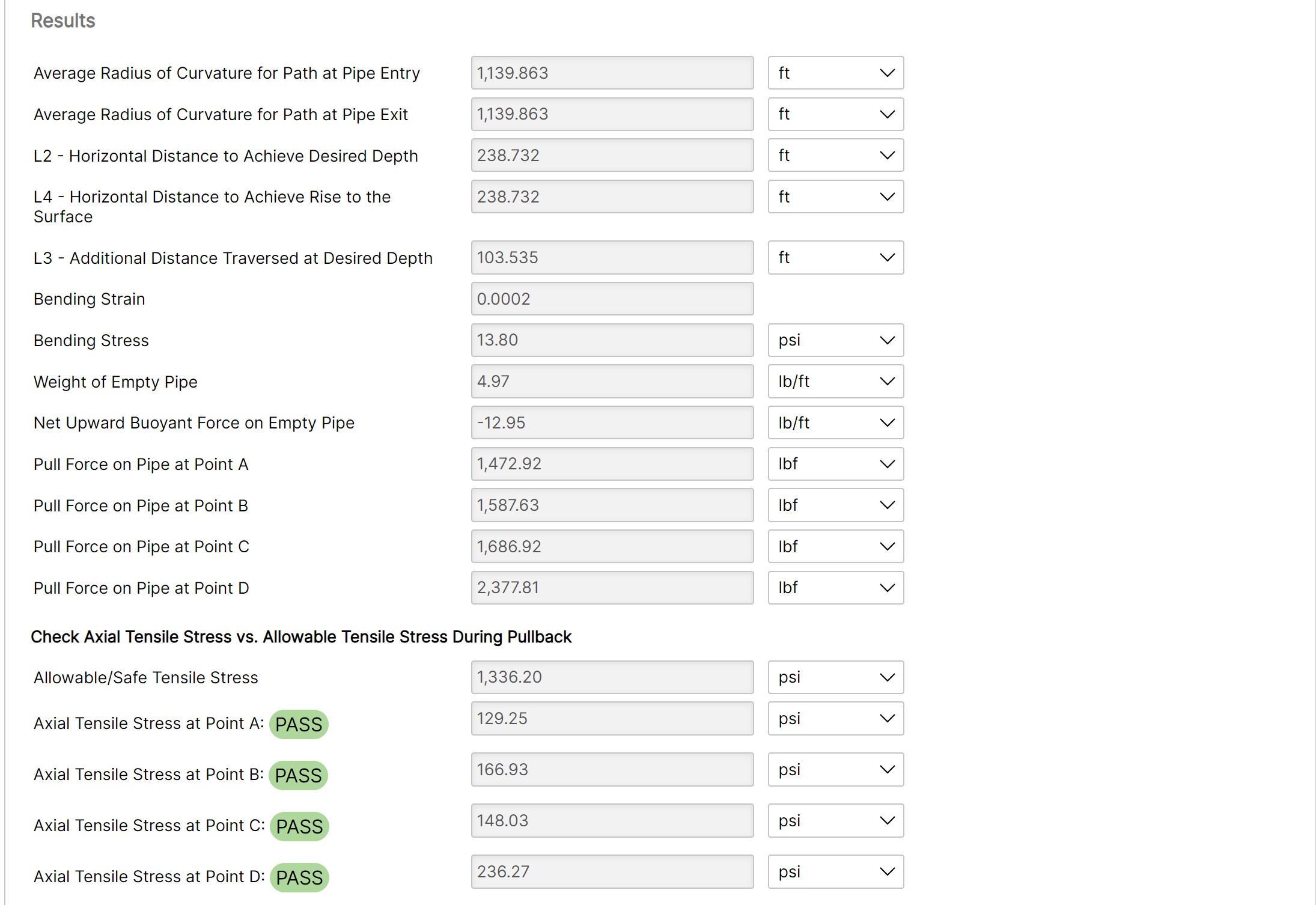
• Average radius of curvature for path at pipe entry (ft)
• Average radius of curvature for path at pipe exit (ft)
• L₂ – Horizontal Distance to Achieve Desired Depth (ft)
• L₄ – Horizontal Distance to Achieve Rise to the Surface (ft)
• L₃ – Additional Distance Traversed at Desired Depth (ft)
• Bending Strain
• Bending Stress (psi)
• Weight of Empty Pipe (lb/ft)
• Net Upward Buoyant Force on Empty Pipe (lb/ft)
• Pull Force on Pipe at Point A (lb/ft)
• Pull Force on Pipe at Point B (lb/ft)
• Pull Force on Pipe at Point C (lb/ft)
• Pull Force on Pipe at Point D (lb/ft)

Check Axial Tensile Stress vs. Allowable Tensile Stress During Pullback:

• Allowable/Safe Tensile Stress (psi)
• Axial Tensile Stress at Point A (psi)
• Axial Tensile Stress at Point B (psi)
• Axial Tensile Stress at Point C (psi)
• Axial Tensile Stress at Point D (psi)
• Breakaway Links Settings (lbf)
• Static Head Pressure (psi)
• Maximum Pressure During Pullback (psi)
• Ovality Compensation Factor
• Tensile Reduction Factor
• Critical Collapse Pressure (psi)
• Safety Factor Against Collapse (psi)

References

• Willoughby, David (2005). Horizontal Directional Drilling, McGraw-Hill, New York, ISBN 0-87814-395-5. v.
• Willoughby, David, Training – Horizontal Directional Drilling, TTI, November 2016
• HDD Consortium. (2001). Horizontal directional drilling, good practices guidelines, HDD Consortium.
• Horizontal Directional Drilling Training Manual, Horizontal Drilling International, February 1999
• Skonberg, Eric R. II. Muindi, Tennyson M. (2014). Pipeline Design for Installation by Horizontal Directional Drilling, American Society of Civil Engineers. Horizontal Directional Drilling Design Guideline Task Committee.
• “Installation of Pipelines by Horizontal Directional Drilling”, PRCI Report PR-227-9424
• Nayyar, Mohinder L. (1992). Piping Handbook, 6th Edition, McGraw-Hill, New York, NY.
• AWWA (2006), PE Pipe Design and Installation, M55, American Water Works Association, Denver, CO
• ASTM (1962), PPI Handbook

FAQ