Introduction
This application uses a positive displacement compressor model to deliver gases at high pressures. With piston displacement reciprocating compressors, often final outlet temp could be a concern.
Piston Displacement
Single-Acting Piston Compression on the Outer End Only: PD = \frac{sn\pi D^2}{4 \times 1728}
PD = \frac{sn\pi D^2}{4 \times 1728}
Single-Acting Piston Compression on the Crank End Only: PD = \frac{sn\pi (D^2 – d^2)}{4 \times 1728}
PD = \frac{sn\pi (D^2 - d^2)}{4 \times 1728}
Double-Acting Piston Compression (Other than Tail Rod Type): PD = \frac{sn\pi (2D^2 – d^2)}{4 \times 1728}
PD = \frac{sn\pi (2D^2 - d^2)}{4 \times 1728}
Double-Acting Piston Compression (With a Tail Rod): PD = \frac{2sn\pi (D^2 – d^2)}{4 \times 1728}
PD = \frac{2sn\pi (D^2 - d^2)}{4 \times 1728}
Where:
ππ· β Piston Displacement (ft3/min)
π β Stroke (ππ)
π β Rotational Speed (rpm)
π· β Cylinder Inside Diameter (in)
π β Piston Rod Diameter (in)
Reciprocating Compressor Volumetric Efficiency
VE = 100 – A – L_u – r – C \left[ \frac{Z_s}{Z_d} \left( r^{\frac{1}{k}} \right) – 1 \right]
VE = 100 - A - L_u - r - C \left[ \frac{Z_s}{Z_d} \left( r^{\frac{1}{k}} \right) - 1 \right]
Where:
ππΈ β Volumetric Efficiency (%)
π΄ β Effect of Leakage, Losses etc. (%)
πΏπ’ β Effect due to Lack of Lubrication (%)
π β Compression Ratio (π2/π1)
πΆ β Cylinder Clearance as a Percent of Cylinder Volume (%)
π§π β Compressibility Factor at Suction Conditions
π§π β Compressibility Factor at Discharge Conditions
π β Adiabatic/Isentropic Exponent (ππ/ππ£)
In practice for normal operation
VE = 96 – r – C \left[ \frac{Z_s}{Z_d} \left( r^{\frac{1}{k}} \right) – 1 \right]
VE = 96 - r - C \left[ \frac{Z_s}{Z_d} \left( r^{\frac{1}{k}} \right) - 1 \right]CNGA/GPSA Compressibility Factor Approximation:
Z=\frac{1}{\left[1+\left(\frac{3.444\times10^5P\times10^{1.785G}}{T_f^{3.825}} \right)\right]}
Z=\frac{1}{\left[1+\left(\frac{3.444\times10^5P\times10^{1.785G}}{T_f^{3.825}} \right)\right]}Where:
π β Compressibility Factor
π β Pressure
ππ β Gas Flowing Temperature (Β°π
)
This approximation will produce results sufficiently accurate for preliminary calculations.
Q_{\text{actual}} = PD \frac{VE}{100} \quad [\text{ft}^3/\text{min}] \text{(ACFM)} \~\ Q_{\text{actual}} = PD \cdot VE\frac{P_1}{P_b} \cdot 14.4 \times 10^{-5} \quad [\text{MMCFD}] \~\ Q_{st} = Q_{\text{actual}} \frac{P_1}{P_b}\frac{T_b}{T_1}\frac{Z_b}{Z_1} \quad [\text{MMSCFD}]
Q_{\text{actual}} = PD \frac{VE}{100} \quad [\text{ft}^3/\text{min}] \text{(ACFM)} \\~\\ Q_{\text{actual}} = PD \cdot VE\frac{P_1}{P_b} \cdot 14.4 \times 10^{-5} \quad [\text{MMCFD}] \\~\\ Q_{st} = Q_{\text{actual}} \frac{P_1}{P_b}\frac{T_b}{T_1}\frac{Z_b}{Z_1} \quad [\text{MMSCFD}]
Reciprocating Compressor Horsepower
HP=\frac{144}{33000}\left( \frac{P_1Q}{n}\right)\left(\frac{k}{k-1} \right)\left[ (r)^{\frac{k-1}{k}}-1\right] [HP]
HP=\frac{144}{33000}\left( \frac{P_1Q}{n}\right)\left(\frac{k}{k-1} \right)\left[ (r)^{\frac{k-1}{k}}-1\right] [HP]Where:
π β Suction Capacity (SCFM)
π1 β Gas Suction Pressure (psi)
π β Compressor Efficiency
π = (ππ/ππ£) β Specific Heat Ratio
π β Compression Ratio (π2/π1)
Ideal Discharge Temperature
T_{2(\text{ideal})} = T_1 \left[ (r)^{\frac{k-1}{k}} – 1 \right]
T_{2(\text{ideal})} = T_1 \left[ (r)^{\frac{k-1}{k}} - 1 \right]
Where:
π2(πππππ) β Ideal Discharge Temperature (Β°R)
π1 β Suction Temperature (Β°R)
π β Compression Ratio (P2/P1)
π β π΄diabatic/Isentropic Exponent (π=[ππ/ππ£])
Theoretical Discharge Temperature
\Delta T_{\text{ideal}} = T_1 \left[ (r)^{\frac{k-1}{k}} – 1 \right]
\Delta T_{\text{ideal}} = T_1 \left[ (r)^{\frac{k-1}{k}} - 1 \right]
Where:
π2 = π1+Ξππππππ
π2 β Theoretical Discharge Temperature (Β°R)
Actual Discharge Temperature
\Delta T_{\text{actual}} = T_1 \frac{\left[ (r)^{\frac{k-1}{k}} – 1 \right]}{ {n_a}}
\Delta T_{\text{actual}} = T_1 \frac{\left[ (r)^{\frac{k-1}{k}} - 1 \right]}{ {n_a}}
Where:
π2 = π1+Ξππππ‘π’ππ
π2 β Actual Discharge Temperature (Β°R)
ππ β Adiabatic (Isentropic) Efficiency
Case Guide
Part 1: Create Case
- Select the Adiabatic Head application from the Compressor Module
- To create a new case, click the βAdd Caseβ button
- Enter Case Name, Location, Date and any necessary notes.
- Fill out all required Parameters.
- Make sure the values you are inputting are in the correct units.
- Click the CALCULATE button to overview results.
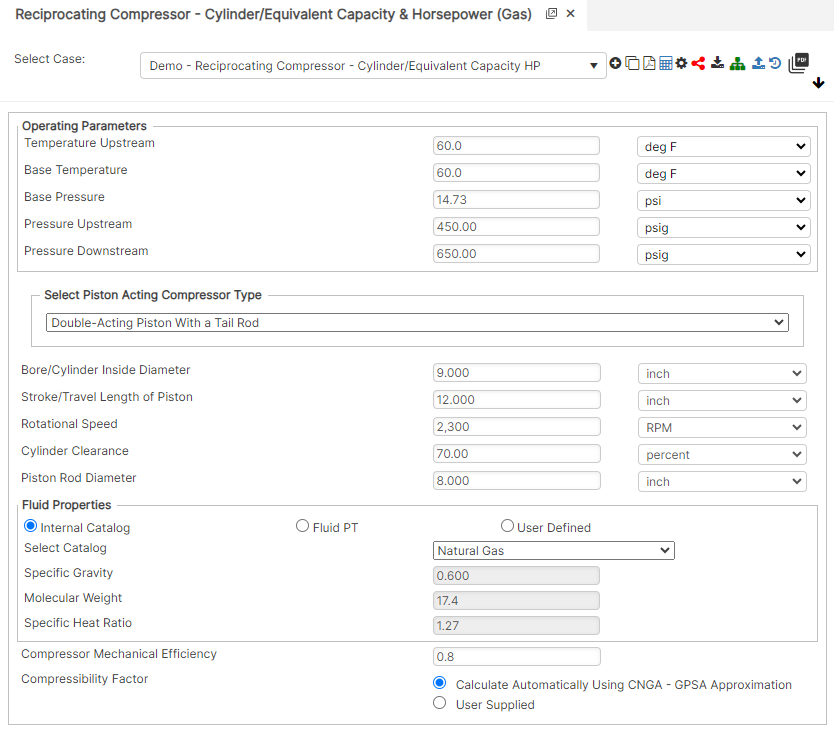
Input Parameters
- Suction Temperature Upstream (Β°F)
- Base Temperature (Β°F)
- Base Pressure (psi)
- Suction Pressure Upstream (psig)
- Discharge Pressure Downstream (psig)
- Bore/Cylinder Inside Diameter (in)
- Stroke/Travel Length of Piston (in)
- Rotational Speed (rpm)
- Cylinder Clearance (%)
- Piston Rod Diameter (in)
- Capacity/Required Flow Rate (MMSCFD)
- Gas Specific Gravity (Relative to air)
- Gas Molecular Weight
- Gas Specific Heat Ratio
- Compressor Mechanical Efficiency
- Compressibility Factor
Part 2: Outputs/Reports
- If you need to modify an input parameter, click the CALCULATE button after the change.
- To SAVE, fill out all required case details then click the SAVE button.
- To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
- To generate a REPORT, click the REPORT button.
- The user may export the Case/Report by clicking the Export to Excel icon.
- To delete a case, click the DELETE icon near the top of the widget.
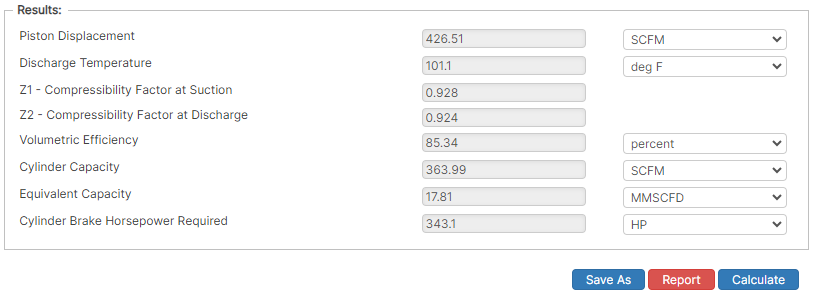
Results
- Piston Displacement (ftΒ³/min)
- Discharge Temperature (Β°F)
- Z1 – Compressibility Factor at Suction
- Z2 – Compressibility Factor at Discharge
- Volumetric Efficiency (%)
- Cylinder Capacity (SCFM)
- Equivalent Capacity (MMSCFD)
- Cylinder Brake Horsepower Required (HP)
References
- Engineering Data Book, Volume 1, Gas Processors Suppliers Association, Tenth Edition
- Compressor Station Operation, Book T-2, GEOP, American Gas Association (A.G.A.)
- Compressor Selection and Sizing, Royce N. Brown, Second Edition, Gulf Professional Publishing