Introduction
The Track Load Program was designed to calculate the overburden and track loads on buried pipe with a Single Layer System (soil only). The information used to design this program was taken from the Newmark’s Integration of the Boussinesq Equation which considered the theoretical work done by M.G. Spangler on overburden and vehicle loads on buried pipe. This analysis does not evaluate cyclic loading, but the API 1102 calculation does.
Variables and Boundary Conditions
REQUIRED INFORMATION:
- Values for all the following variables:
- 𝐻2 −Cover, Vertical Depth from the Ground to the Top of the Pipe (ft.)
- 𝐵 − Trench Width (ft.)
- 𝐷𝑠 − Weight per unit Volume of Backfill (lbs/ft3)
- 𝐷 − Outside Diameter of the Pipe (in.)
- 𝑆𝑀𝑌𝑆 − Specified Minimum Yield Stress of the Pipe (psi.)
- 𝑃 − Pipe Internal Pressure (psi.)
- 𝑇 − Pipe Wall Thickness (in.)
- Variables for the following information about the track:
- 𝐿𝑡 − Operating Weight of the Object Crossing the Pipeline with Tracks(lbs)
- 𝑇𝑤 − Width of the Standard Track Shoe(in)
- 𝑇𝑙 − Length of the Track on the Ground(ft)
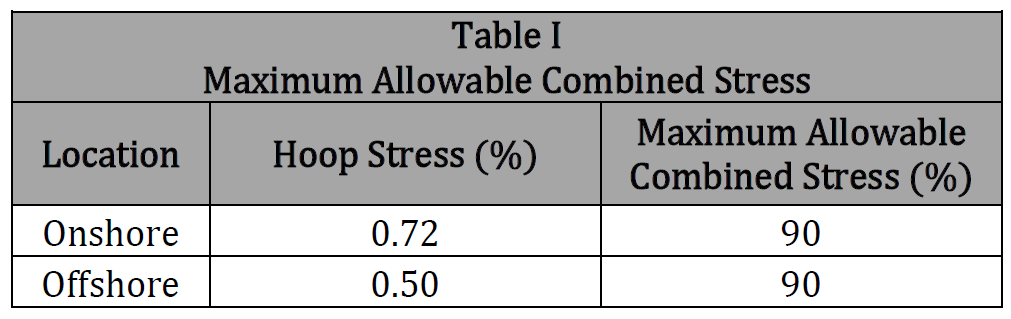
- The Design Factor of the pipeline being analyzed is used to find the Maximum Allowable Combined Stress (% SMYS), (0.72 is the standard factor used for liquid).
- The Soil Type which is used to find the friction force coefficients (Km), see Table II.
- The Crossing Construction Type which is used to find the bedding constants for buried pipe (Kb & Kz), see Table V & Figure 3.
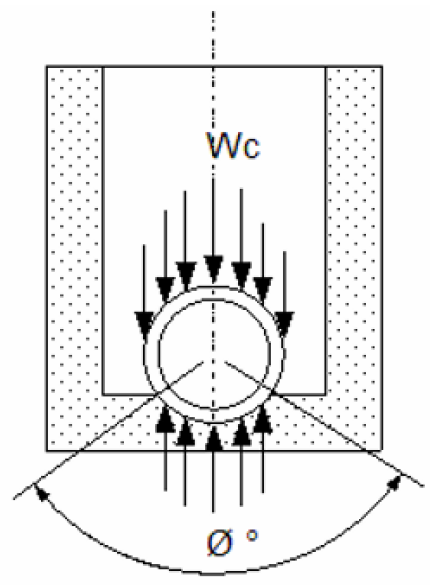
- All the above information along with values for the following variables:
- X – Longitudinal Distance over which Deflection Occurs (ft)
- Y – Vertical Deflection (in)
Workflow
As a first estimate of the soil load on the pipe it could be assumed that the backfill soil slides down the trench walls without friction. Additionally, assume that all soil above the pipe is supported by the pipe itself and that the backfill soil on either side of the pipe does not assist in this support.
These assumptions are very conservative, but they help a great deal in initial understanding of the method of solution. The assumptions yield a soil load on the pipe equal to the weight of the backfill soil above the pipe. This analysis provides an estimate of soil loads on the buried pipe if nothing else is known about the system.
The basic analysis developed by M.G. Spangler follows similar arguments to that given above. In this analysis, Spangler includes frictional forces between the trench wall and the backfill. This permits the weight of the overburden to be partially carried by the surrounding soil and reduces the total soil load on the pipe. The resulting equations for calculating the pipe load due to overburden are as follows:
Which is used to find the friction force coefficients (Km)
C_d = \frac{1 – e^{(-2K_{\mu}(H_2/B))}}{2K_{\mu}}
C_d = \frac{1 - e^{(-2K_{\mu}(H_2/B))}}{2K_{\mu}}
- 𝐶𝑑 − Trench Coefficient
- 𝐵 − Trench Width(ft)
- 𝐻2 − Cover, vertical depth from the ground surface to top of pipe(ft)
- 𝐾𝜇 − Coefficient of friction force between the backfill soil and the trench wall.
Cd determines how much load is carried by the pipe. If there is no soil friction Cd becomes equal to H/B and the entire backfill load must be supported by the pipeline. The term Kμ provides a coefficient of friction force between the backfill soil and the trench wall. A high value of Kμ implies that friction between the backfill and trench wall is high and the weight of the backfill is supported largely by the wall friction. A low value implies that there is little friction encountered and the backfill is allowed to settle more such that the weight must be supported by the pipe. Table II provides values of Kμ used in the program for five different soil types. Also, in Table II are examples of values for Ds, the density which is the weight per unit of backfill, which may be used if an actual value is not known.
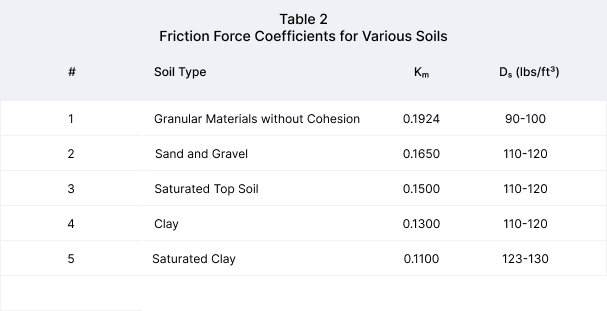
The soil types and coefficients given in this table represent the range that could normally be expected. Saturated clay has little internal friction so that it has the smallest value for Kμ. This implies that almost all of the soil load is carried by the pipe. Granular materials have a great deal more internal friction. Their value of Kμ is higher which leads us to the conclusion that the pipe carries less of the backfill load. Spangler, in his work, recommends using the value for clay in most instances. Higher values may be used when there is adequate evidence that the internal friction is higher and warrants a higher value of Kμ.
Spangler’s recommendation provides a conservative estimate for common buried pipe situations. Marsh and bog areas, however, have friction properties more similar to saturated clay such that a value for Km equal to 0.110 should be used in these areas.
W_c = \frac{1 – e^{(-2K_{\mu}(H_2/B))}}{2K_{\mu}} D_s B^2(0.833)
W_c = \frac{1 - e^{(-2K_{\mu}(H_2/B))}}{2K_{\mu}} D_s B^2(0.833)
- 𝑊𝑐 − Load per unit Length of the Pipe due to Overburden(lbs/in)
- 𝐵 − Trench Width(ft)
- 𝐻2 − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)
- 𝐷𝑠 − Density which is the Weight per unit of Backfill(lbs/ft3)
- 𝐾𝜇 − Coefficient of Friction Force between the Backfill Soil and the Trench Wall.
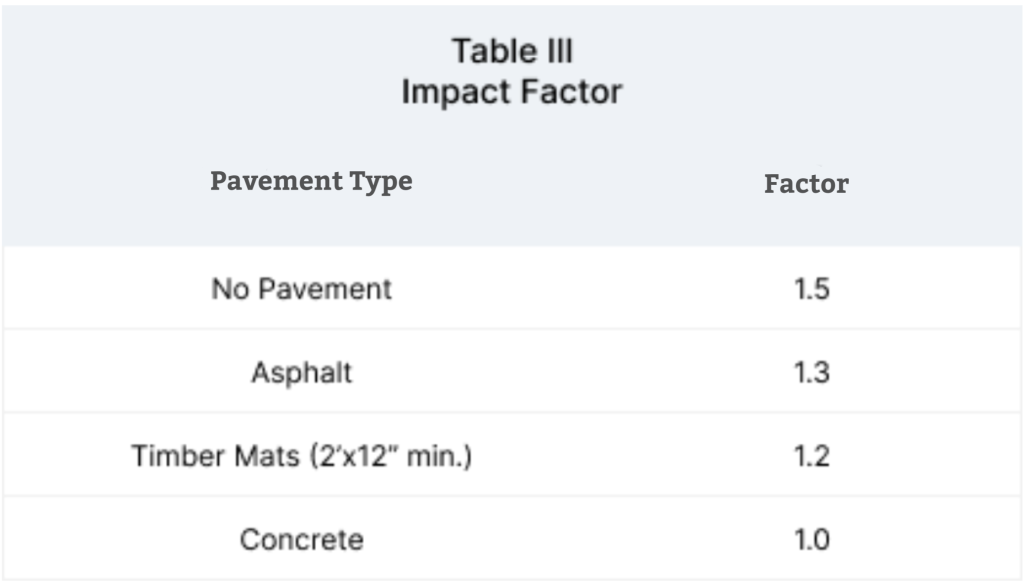
The Impact Factor (I) for a track load calculation with a single layer system is always going to be 1.5. The reason for this is that the impact factor for soil is 1.5 and that is the only thing that separates the track from the pipe in a single layer system.
Calculating track load is somewhat different from calculating a wheel load because the load of a track expands over a larger area rather than a single point as does the wheel load. The information needed from the track are the operating weight (Lt) of the object crossing the pipeline with tracks is measured in lbs., the width of the standard track shoe (Tw) measured in inches, the length of the track on the ground (Tl) measured in ft., and the track gauge (Tg) measured in ft.
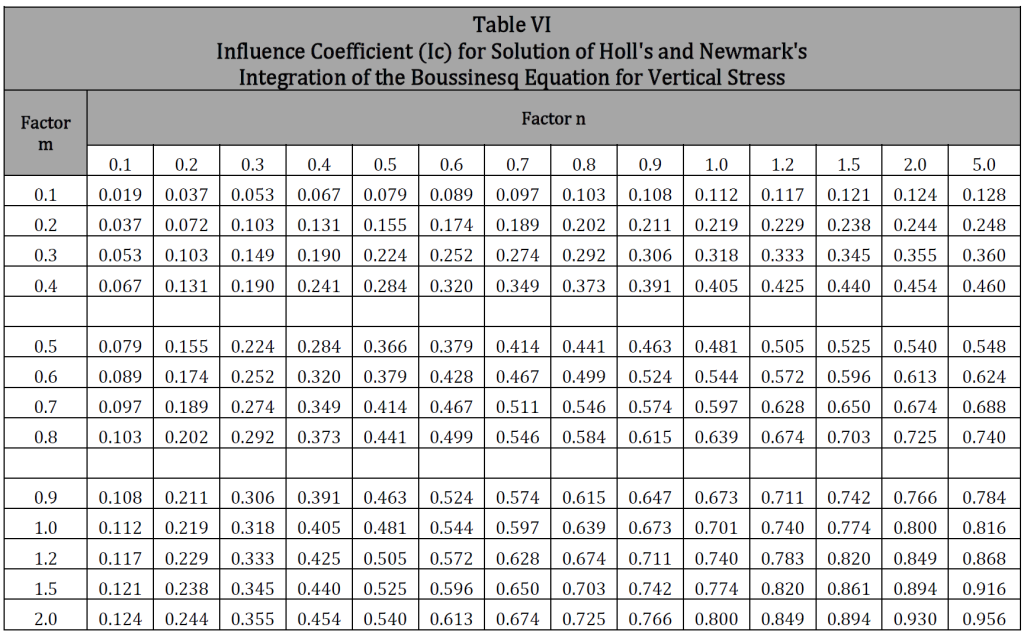
The weight of a track can be considered as a uniformly distributed load applied at the top of the soil over an area equal to the length of the track on the ground times the width of the standard track shoe. On the basis of this assumption, the unit pressure at a point on the top of the line pipe or casing pipe directly beneath the center of the area may be estimated by means on Newmarks Integration of Boussinesq equation. Newmark determined the pressure at a point in the undersoil at any elevation below one corner of the rectangular area over which unit loads are uniformly applied and gave influence coefficients corresponding to the Influence Factor m and Influence Factor n.
\text{Influence Factor } m = \frac{T_w}{2H_2(12)}
\text{Influence Factor } m = \frac{T_w}{2H_2(12)}
- 𝐻2 − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)
- 𝑇𝑤 − width of the standard track shoe(in)
\text{Influence Factor } n = \frac{T_l}{2H_2}
\text{Influence Factor } n = \frac{T_l}{2H_2}
- 𝐻2 − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)
- 𝑇𝑙 − Length of the track on the ground(ft)
These two factors are used by M.G. Spangler in the table called “Influence Coefficients for Solution of Holl’s and Newmark’s Integration of the Boussinesq Equation for Vertical Stress”, see Table VI. Both of the influence factors will be rounded off to the nearest 0.01 in order to cross reference Table VI.
Q_d = \frac{(0.5L_t)}{\left( \frac{T_w}{12} T_l\right)} I_c
Q_d = \frac{(0.5L_t)}{\left( \frac{T_w}{12} T_l\right)} I_c
- 𝑄𝑑 − Maximum static pressure on the pipe directly under the center of the object with tracks(lbs/ft2)
- 𝐼𝑐 − Influence Coefficient selected from Table IV
- 𝐿𝑡 − Operating weight of the object crossing the pipeline with tracks(lbs)
- 𝑇𝑤 − Width of standard track show(in)
W_t=\frac{IQ_d}{12}\frac{D}{12}
W_t=\frac{IQ_d}{12}\frac{D}{12}- 𝑊𝑡 − Total track load on the pipe(lbs/in)
- 𝐷 − Outside diameter of the pipe(in)
- 𝐼 − Impact factor
- 𝑄𝑑 − Maximum static pressure on the pipe directly under the center of the object with tracks(lbs/ft2)
S_c= \left( W_c + W_t \right) \left( \frac{3K_bEDT}{ET^3 + 3K_zPD^3} \right)
S_c= \left( W_c + W_t \right) \left( \frac{3K_bEDT}{ET^3 + 3K_zPD^3} \right)
- 𝑆𝑐 − Circumferential stress due to pipe wall deflection(psi)
- 𝐷 − Outside Diameter of the pipe(in)
- 𝐸 − Pipe material modulus of elasticity (2.9 x 107)
- 𝐾𝑏 − Bending coefficient which is a function of the crossing construction types
- 𝐾𝑧 − Deflection coefficient which is a function of the crossing construction types
- 𝑃 − Pipe internal pressure (psi)
- 𝑇 − Pipe wall thickness(in)
- 𝑊𝑐 − Load per unit length of pipe due to overburden(lbs/in)
- 𝑊𝑡 − Total track load on pipe(lbs/in)
Equation Sc, as well as equation St, have two constants which depend upon the bedding material upon which the pipe is placed. This bedding material is based on the crossing construction type. When the pipe is placed on a rigid bedding such as an Open Cut-Rock, little soil deformation occurs so that the load application area on the bottom is very small.
However, if the pipe is placed on soil, the support conforms to the pipe somewhat and the load is distributed over a larger area (See Figure 3). The latter case produces less pipe stress and is preferable. Spangler’s formulation includes both of these possibilities in order to provide a conservative estimate for the rigid bedding case without penalizing the soil bedding case. It does so by varying the constants Kb and Kz. Spangler’s recommended values for the constants are provided in Table V.

S_h=\frac{PD}{2T}
S_h=\frac{PD}{2T}- 𝑆ℎ − Hoop Stress due to Internal Pressure(psi)
- 𝐷 − Outside Diameter of the Pipe(in)
- 𝑃 − Pipe Internal Pressure(psi)
- 𝑇 − Pipe Wall Thickness(in)
S_t = \left( \frac{PD}{2T} \right) + \left( W_c + W_v \right) \left( \frac{3K_bEDT}{ET^3 + 3K_zPD^3} \right)
S_t = \left( \frac{PD}{2T} \right) + \left( W_c + W_v \right) \left( \frac{3K_bEDT}{ET^3 + 3K_zPD^3} \right)
St is the total circumferential stress in the pipe wall due to pressure (hoop) stress and bending stresses resulting from circumferential flexure caused by external loads measured in PSI. The first term on the right-hand side of the equation is the formula for hoop stress due to internal pressure (Sh) and the second term is the formula for circumferential stress due to pipe wall deflection (Sc). Longitudinal Bending Stress (Sb) is when the overburden and vehicle load on buried pipelines will cause pipe settlement into the soil in the bottom of the trench. This settlement occurs because soil is not as stiff as the pipe and will deform easily as the pipe is “pushed” downward. Under uniform soil conditions and overburden loading, the pipe will settle evenly into the trench bottom along its entire length. Soil is not generally uniform, however, and regions of “softer” soil will occur adjacent to regions of stiff soil, so that the pipe will settle unevenly and hence bending will occur. A load that is applied on only one portion of a pipeline will cause the section of pipe under the load to settle more than the unloaded pipe, such that bending will also result. Longitudinal bending stress occurs in tension on the outside of the bend and in compression on the inside of the bend. Tensile stress is represented with a positive value for Sb; conversely, compressive stress takes a negative value for Sb. The longitudinal bending stress is calculated as follows: S_b=\frac{EDY}{48X^2}
S_b=\frac{EDY}{48X^2}- 𝑆𝑏 − Longitudinal Bending Stress(psi)
- 𝐷 − Outside Diameter of the Pipe(in)
- 𝐸 − Pipe Material Modulus of Elasticity(2.9 x 107)
- 𝑋 − Longitudinal Distance over which Deflection occurs(ft)
- 𝑌 − Vertical Deflection(in)
A negative value will be used when calculating the total combined stress (S). This will result in a larger (more conservative) combined stress. Note: If longitudinal bending stress does occur, click onto the designated box next to “Longitudinal Bending Stress”. If the box is not marked, then the program will assume “0” for Sb.
S = \sqrt{(S_t^2 – S_tS_b + S_b^2)}
S = \sqrt{(S_t^2 - S_tS_b + S_b^2)}
- 𝑆 − Total Combined Stress by Von Mises(psi)
- 𝑆𝑏 − Longitudinal Bending Stress(psi)
- 𝑆𝑡 − Total Circumferential Flexure caused by External Loads(psi)
\%SMYS=\frac{S}{SMYS}
\%SMYS=\frac{S}{SMYS}- S – Total Combined Stress by Von Mises(psi)
- SMYS – Specified Minimum Yield Strength(psi)
Case Guide
Part 1: Create Case
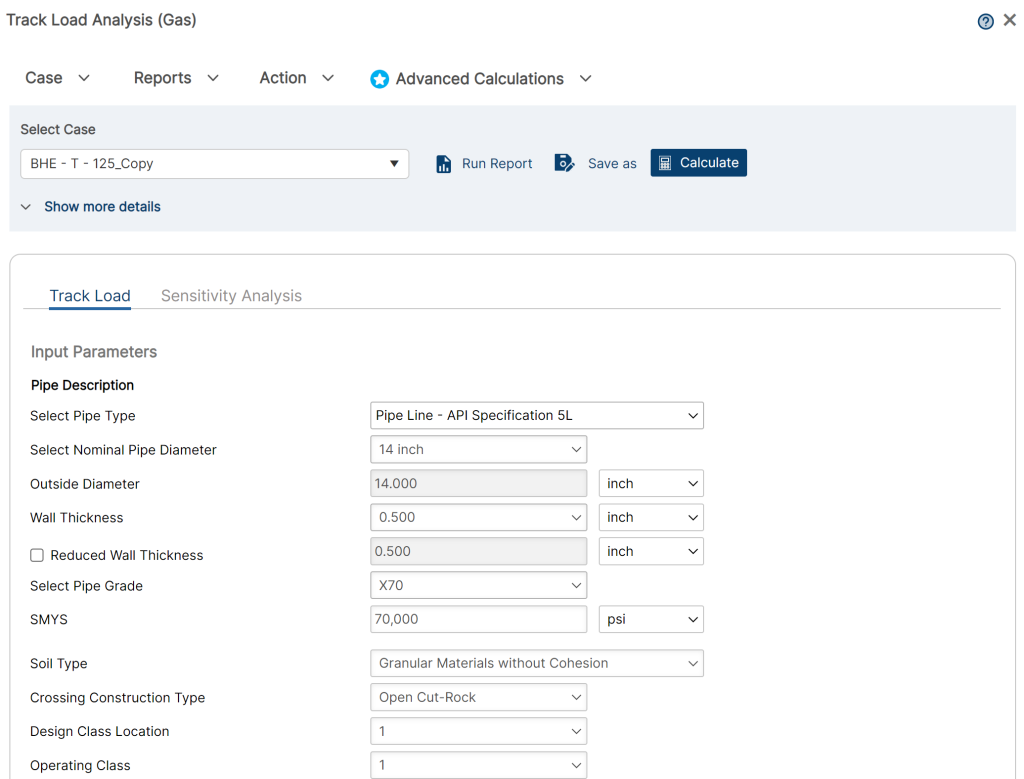
- Select the Track Load Analysis application from the Pipeline Crossing module
- To create a new case, click the “Add Case” button
- Enter Case Name, Location, Date and any necessary notes.
- Fill out all required Parameters.
- Make sure the values you are inputting are in the correct units.
- Click the CALCULATE button to overview results
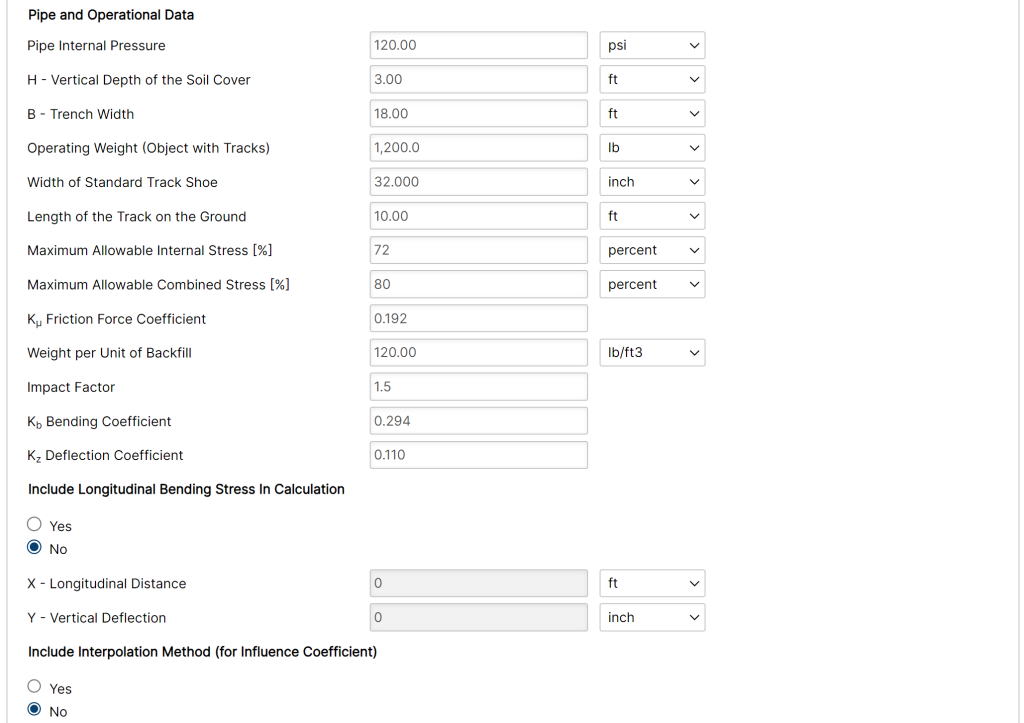
Input Parameters
- Nominal Pipe Size(in):(1/8” – 48”)
- Pipe Outside Diameter(in):(0.625” – 48”)
- Pipe Wall Thickness(in):(0.068”- >2”)
- Design Location
- Operation Class
- Soil Type
- Crossing Construction Type
- Maximum Allowable Internal Stress
- Maximum Allowable Combined Stress
- Friction Force Coefficient
- Weight Per Unit of Backfill
- Impact Factor
- Bending Coefficient
- Deflection Coefficient
- Pipe Internal Pressure
- Operating Weight
- Vertical Depth of the Soil Cover
- Width of Standard Track Shoe
- Trench Width
- Specified Minimum Yield Stress:(24000psi-80000psi)
- Length of the Track on Ground
- Include Longitudinal Bending Stress in Calculation
- X – Longitudinal Distance
- Y – Vertical Deflection
- Include Extrapolation Method (for Influence Coefficient)
Part 2: Outputs/Reports
- If you need to modify an input parameter, click the CALCULATE button after the change.
- To SAVE, fill out all required case details then click the SAVE button.
- To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
- To generate a REPORT, click the REPORT button.
- The user may export the Case/Report by clicking the Export to Excel icon.
- To delete a case, click the DELETE icon near the top of the widget.
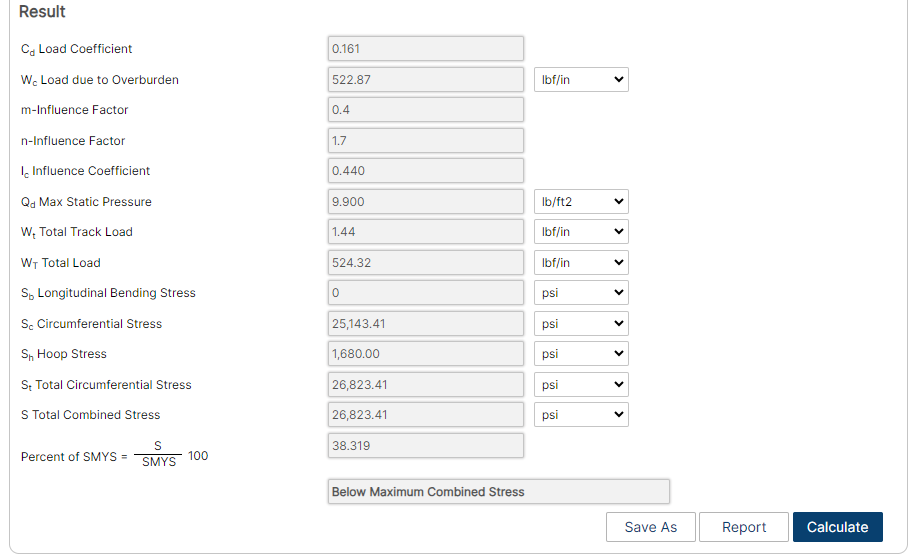
Results
- Load Coefficient
- Load due to Overburden
- m – Influence Factor
- n – Influence Factor
- Influence Coefficient
- Maximum Static Pressure
- Total Track Load
- Total Load
- Longitudinal Bending Stress
- Circumferential Stress
- Hoop Stress
- Total Circumferential Stress
- Total Combined Stress
- Percent Of SMYS
- Status
Reference
- Battelle Petroleum Technology Report on “Evaluation of Buried Pipe Encroachments” which considered the theoretical work done by M.G. Spangler on overburden and vehicle loads on buried pipe.
- “Technical Summary and Database for Guidelines for Pipelines Crossing Beneath Railroads and Highways” (GRI-91/0285, Final Report)
- Cornell/GRI Guidelines are given in “Guidelines for Pipelines Crossing Beneath Highways” (Stewart, et al., 1991b) and “Guidelines for Pipelines Crossing Beneath Highways”.
- ASME B31.8 “Gas Transmission and Distribution Systems” “Evaluation of Buried Pipe Encroachments”, BATTELLE, Petroleum Technology Center, 1983
- API RP 1102 – Steel Pipelines Crossing Railroads and Highways
FAQ
-
What are crossings – Live Load?
Many questions are asked about API 1102 regarding wheel load cyclic stresses on highways and railroads.
Live highway load, w, the load due to the wheel load at the highway surface. The load from only one wheel set needs to be considered. An axle is considered to have two-wheel sets.
Live rail load, w, pounds per sq inch, is the load applied at the surface of the crossing. It is assumed that the load is evenly distributed over an area that is 8’x 20’.The recommended default is 80,000 pounds (80 Kips) per axle. Check Out
-
Validation checks in place for API 1102 – Pipeline Crossing Railroad?
Below are the list of validation checks we have incorporated in API 1102 – Pipeline Crossing Railroad (Gas and Liquid). Check Out
-
Validation checks in place for API 1102 – Pipeline Crossing Highway?
Below are the list of validation checks we have incorporated in API 1102 – Pipeline Crossing Highway (Gas and Liquid). Check Out
-
Track Load – Interpolation Method (for Influence Coefficient)?
We recently issued an enhancement for Track load calculation by providing an option to use the Interpolation Method to calculate the Influence Coefficient (Ic). The old method calculated the Influence Coefficient using a roundoff method for ‘m-Influence Factor’ and ‘n-Influence Factor’ to get the Influence Coefficient from the table. Check Out
-
API 1102 Uncased Crossing 10 Foot Limit Understanding?
Uncased carrier pipe is subjected to internal loading from pressure and external loading from earth loading (dead load) and live (cyclic) loading from highway or railroad traffic. Other loading due to special or temporary conditions should be evaluated on the specific situation in the field (See Knowledge Base Article for Temporary Conditions). Check Out
-
Surface Load Mitigation Measures – Best Practice?
Method
Reduce the operating pressure of the pipeline.
Advantages
Provides a direct reduction of the hoop stress due to internal pressure. This reduction allows for additional circumferential stress due to equipment loads.
Disadvantages
– Reduces the beneficial effect of internal pressure on the pipe circumferential bending stresses due to fill and traffic loads.
– Could reduce the overall capacity of the pipeline and therefore should not be considered as a long term fix.
-
Difference between “Operating Weight” in Track Load Analysis and “concentrated surface load” in Wheel Load?
The term “Operating Weight” used in the track load analysis is a straight forward analysis as it takes the total weight of the equipment into consideration. We multiply the total weight by 0.5 to reflect the load on each track (see below the equation).
“Concentrated surface load” in the Wheel load calculation requires a more detailed understanding of the vehicle that is crossing. Below schematic will help better understand the requirement for “Concentrated surface load” entry in Wheel Load analysis.
-
Determining Trench Width for Crossings?
The basic analysis developed by M.G. Spangler includes frictional forces between the trench wall and the backfill. This permits the weight of the overburden to be partially carried by the surrounding soil and reduces the total soil load on the pipe. The equations require the following information to determine internal friction. Check Out
-
Combined Stress for Wheel Load and Track Load?
The question comes up from time to time how to address local stresses for wheel and track load calculations. ASME B31.8 833.9 Local Stresses states that the maximum allowable sum of circumferential stress due to internal pressure (Barlow Design Formula) and circumferential through-wall bending stress caused by surface vehicle loads or other local loads is 0.9ST, where S is the specified minimum yield strength, psi (MPA) per para. 841.1 (a), and T is the temperature derating factor per para. 841.1.8. Check Out
-
What Are Timber Mats in Crossing?
Timber mats are used for temporary access roads, work pads, staging areas, and to stabilize the ground beneath heavy equipment, dissipating heavy loads and providing equipment stability.
For short-term water crossings over narrow spans timber mats (also referred to as bridge mats) or crane mats may be an option.
For projects that require moving heavy equipment safely across pipelines, timber mats can be used to create air bridges which will support the weight of heavy equipment while protecting the pipelines below. Air bridges can also be used to cross culverts, ditches, or sensitive ground that needs to be bridged. Check Out
-
Redistributing Wheel and Track Loads (Pavement and Other Materials)?
This knowledge base article is a takeoff from “Pipeline Toolbox (PLTB) and Vehicles over Buried Pipelines – Maximum Allowable Stress”. These predictions through Spangler’s work, Battelle and others who contributed to validation makes PLTB one of most used programs in the industry. It includes temporary wheel and track load crossings that considers a uniformly distributed load at the surface while calculating the load on the pipe. This article will focus on concrete, asphalt and timber mats as well as other materials such as steel plates and composites. The other materials are not part of the Pipeline Toolbox which will be discussed. Check Out
-
Pipeline Crossings – External Loads and Vehicles over Buried Pipelines “Maximum Allowable Combined Stress”?
This article was created due to the number of inquiries regarding the Maximum Allowable Combined Stress for Class 3 Design Areas. The research by M. G. Spangler, Battelle and industry allowed this information to be a standard practice today with Wheel and Track Load analysis today. Check Out
-
Applicability of Class Location for Liquid Lines? What is the design factor used for Liquid Pipeline Operation?
Design factor specification for Liquid Pipelines are governed by ASME B31.4 Table 402.3.1(a)
Excerpts from B31.4: Check Out
-
Loading Requirements for API 1102 E-80 and E-90 Railroad Crossings?
API 1102 for railroad crossing program is based on the design methodology that has been used in analyzing existing uncased pipelines and designing new uncased pipelines that cross beneath railroads. This API design methodology relates to the train engine (E-80) which is the heaviest load: Check Out
-
What are Cased Crossings?
The pipeline industry begins to experience casing problems such as carrier pipe leaks/failures under road crossings.
- Atmospheric corrosion due to condensation (particularly at elevated temperatures and cold soils)
- Metal to metal shorts
- Electrolytic coupling or contact
Can the casing pipe protect the carrier pipe from external loadings? Check Out
-
Understanding Impact Factors in Pipeline Design (CEPA)
What is an Impact Factor?
An impact factor is a multiplier used in pipeline design to account for the additional stress caused by moving vehicles above the pipeline, compared to static loads. Think of it as a “safety buffer” that accounts for the dynamic nature of traffic. Check Out
