The Development of the Modified B31G Criterion, RSTRENG

Introduction

• The known excess conservatism in the original B31G criterion led to the efforts to develop a less conservative criterion without sacrificing safety. The excesses were understood to be:
  • The expression for flow stress, S
  • The approximation used for the Folias factor “M”
  • The parabolic representation 2/3Ld used for metal loss
  • The inability to consider the strength supplied by the islands of full wall thickness between close arrays of corroded patches
• The modified criterion will allow metal loss anomalies of greater size to remain in service at the current MOP and will require less pressure reduction for cases where the reduced pressure is above 55% of SMYS.

B31G Criterion – Research Objective

Texas Eastern Transmission Corporation and the AGA Pipeline Research Committee conducted research in the late 1960s and early 1970s that resulted in the development of a criterion to evaluate the serviceability of corroded pipe. This research was performed at the Columbus laboratories of Battelle Memorial Institute. This criterion has been included in both the B31.4 and B31.8 design codes and is described in detail in the document, “ANSI/ASME B31G -1984 Manual for Determining the Remaining Strength of Corroded Pipelines.”.

The Initial Research Objectives were:

• Examine fracture initiation behavior as a function of corrosion defect size and internal line pressure that would cause a leak or rupture.
• Search with an understanding that a corrosion defect:
  • Caused by an electrochemical process by which the iron in refined steel returns to a more stable state
  • Results to metal loss at anodic areas
  • Not uniform and homogenous
  • Does not involve mechanical stress
  • Formed by a stress-free process

Research Methodology

• The procedure for evaluating the remaining strength of corroded pipe was developed by pressuring actual corroded pipe to failure. Several hundred, full-size, full-scale tests, using actual field pipe specimens, were conducted. These tests were conducted on all types of defects.
• Semi-empirical mathematical expressions to calculate the pressure strength of corroded pipe materials were developed based on these extensive tests. Though semi-empirical, these mathematical expressions were based on well-established fracture mechanics principles.
• The basic principle is that resistance to fracture is related to the size of the defect and the metal property toughness. The larger the corrosion defect, the lower the failure pressure. The tougher the steel, the larger the defect that can be tolerated.

Analysis Confirmation

• During 1970-71, 47 full-size, full-scale pressure tests to rupture were conducted to evaluate, modify and confirm the mathematical expressions that had been developed to estimate failure pressures.
• The diameters ranged from 16″ through 30″, the wall thickness ranged from .312″ through .375″ and the pipe grade ranged from A-25 through X-52. Based on later test results, the mathematical expressions have been modified and the range of materials has been extended to diameters from 2″ through 60″ and wall thickness from .083″ through 1.25″.
• The test experiments on the corroded pipe indicate that line pipe steels have adequate toughness and that toughness is not a significant factor. The tests indicate that the failure of “blunt” corrosion defects is controlled by their size and flow stress (related to the yield strength) of the pipe material.

Research: Findings and Confirmation

• The test results indicated that pipeline grade steels have adequate toughness and that toughness is not a significant factor in the remaining strength.
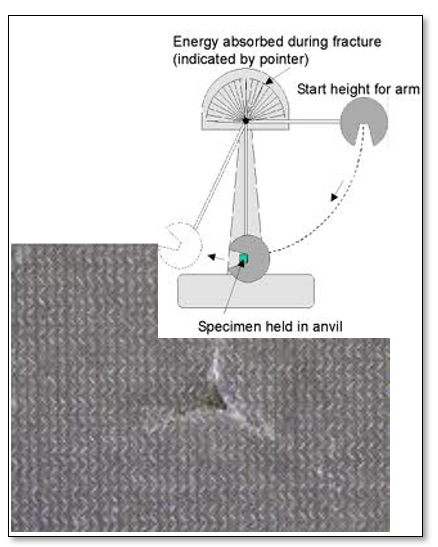
• The tests did indicate that the failure of “blunt” corrosion defects is controlled by their size and the flow stress of the pipe material. Example of blunt defect

Application of the Findings

• Semi-empirical mathematical expressions based on data from these extensive tests were developed to predict the pressure strength of corroded pipe materials.
• During 1970-71, 47 additional full-size, full-scale pressure tests to rupture were conducted on 16″ through 30” pipe with wall thickness ranging from .312″ through .375″ and grades from A-25 through X-52. were made to evaluate, modify and confirm the formulas that had been developed to estimate failure pressures.
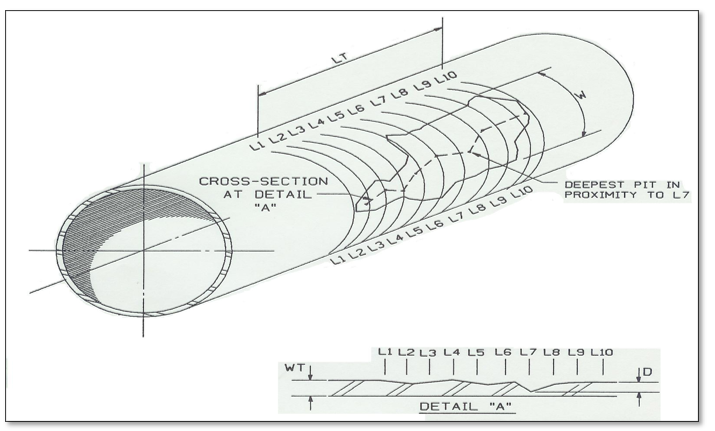
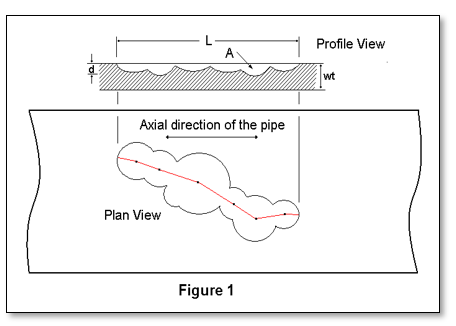• Measurements for the formula factors are taken from a projected profile of the corroded area along the longitudinal axis of the pipe.
• Figure 1: Shows an example profile of how corrosion might occur and how the parameters of metal loss are configured and measured for analysis: L is the projected axial length of corrosion along the longitudinal axis of the pipe, d is the maximum depth of corrosion, wt is the pipe wall thickness and A is the profile of the area of metal loss projected into the axial plane.

B31G Limitations

• Intended for corrosion only on weldable pipeline steels. Applies only to defects that have relatively smooth contours, that is, metal loss due to corrosion.
• No interaction of corroded areas that do not touch.
• Does not evaluate the remaining strength of corroded welds or grooves and gouges caused by mechanical damage.
• The objective is only to evaluate structural integrity under internal pressure, i.e., not secondary stresses.

Factors for B31.G Evaluations

• Original B31G Evaluations

S = 1.1 SMYS

M is a two-term factor = (1+0.8L2/Dt).5 L = axial extent of defect D= pipe diameter t = pipe wall thickness A = (2/3)Ld where d is the maximum pit depth in the profile A0 = Lt

Original B31G Criterion

• With these representations, the equation for predicting the hoop stress which may cause steel pipe to fail was re-written.
  • Sf = 1.1SMYS (1-(2/3)(Ld/Lt))/(1-(2/3)(Ld/Lt)M-1)
  •      = 1.1SMYS (1-(2/3)(d/t))/(1-(2/3)(d/t)M-1)
• This equation referred to as the “Original B31G Criterion”, answered the question “What viable formula would predict the lowest pressure that may cause a corroded area to fail/burst/leak?”

Basis of B31G Criterion

The agreed mathematical expression for predicting failure stress is the equation as shown below and explained in a PRCI Report titled “A Modified Criterion for Evaluating the Remaining Strength of Corroded Pipe”, by John F. Kiefner and Paul H. Vieth:

Sf = S (1 – A/A0)/(1 – (A/A0)M-1)

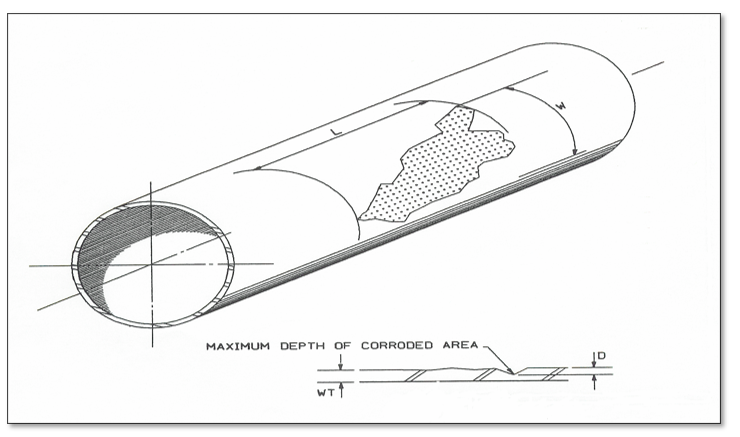
Where: Sf = Hoop stress at failure, psi S = Flow stress of the material, related to the material yield strength, psi A = the defect area in the longitudinal plane, in² A0 = Lt M = Folias factor, a function of L, D, and t L = Axial extent of the defect, inches D = Pipe diameter, inches t = Wall thickness, inches

B31.G & Modified (Max Depth & Length)

RSTRENG Method

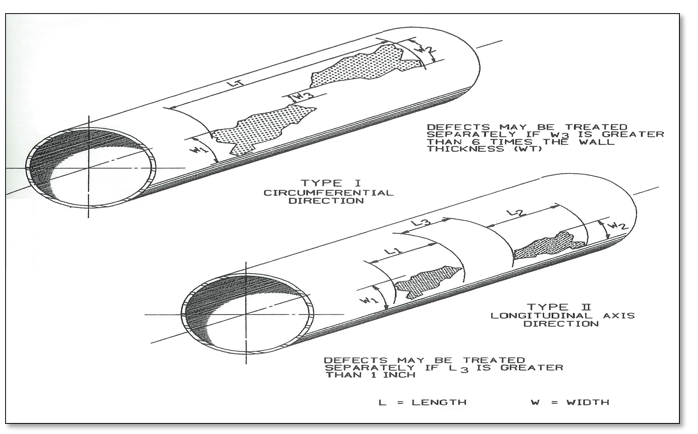
Multiple Pitting Clusters

Related Links