PE Pipe – Pull Force and Installation Stresses (Specific Radius of Curvature)

Specific Radius of Curvature

This procedure is for designing the bore path specific using radius of curvature calculations for plastic pipe that are basically the same as discussed for steel pipe. As with steel product pipe, plastic pipe, when installed by HDD, may experience high-tension loads, severe bending, and external fluid pressures. HDD installation subjects the pipe to axial tensile forces caused by the frictional drag between the pipe and the borehole or drilling fluid, the frictional drag on the ground surface, the capstan effect around drill-path bends, and hydrokinetic drag. The pipe may also be subjected to external hoop pressures caused by the external fluid head and bending stresses. Determination of pullback forces involves the assumption of many variables and installation techniques that include:

Pipe Weight:

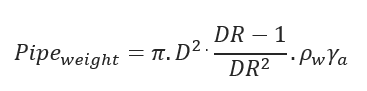
Pipe weight – Weight of the pipe (lbs/ft)
D – Pipe Outside Diameter (inch)
DR – Diameter Ratio (D/t)
𝜌_𝑤 = Density of water (lb/ft3)
𝛾_𝑎 = Specific gravity of pipe material

Pipe Exterior Volume:

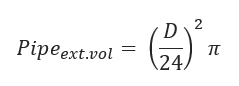
Pipe Interior Volume:

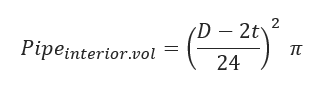
Weight of Water in pipe:

(to be calculated only if the pipe is filled with water)

𝑊𝑎𝑡𝑒𝑟_{𝑃•𝑤𝑒𝑖𝑔ℎ𝑡} = 𝑃𝑖𝑝𝑒_{𝑖𝑛𝑡𝑒𝑟𝑖𝑜𝑟•𝑣𝑜𝑙} ∗𝑊_{𝑤𝑒𝑖𝑔ℎ𝑡}

W_weight – Weight of water (lb/ft3)

Displaced Mud Weight:

𝐷𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑢𝑑_{𝑊𝑒𝑖𝑔ℎ𝑡} = 𝑃𝑖𝑝𝑒_{𝑒𝑥𝑡.𝑣𝑜𝑙} 𝑚𝑢𝑑_𝑤𝑡

mud_wt = Weight of mud (lb/ft3)

Effective Weight of Pipe:

𝑤_𝑎 = 1.06 𝑃𝑖𝑝𝑒_{𝑤𝑒𝑖𝑔ℎ𝑡}

𝑊_𝑆 = 𝑤_𝑎 + 𝑊𝑎𝑡𝑒𝑟_{𝑃•𝑤𝑒𝑖𝑔ℎ𝑡} − 𝐷𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑢𝑑_{𝑊𝑒𝑖𝑔ℎ𝑡}

Hydrokinetic Force:

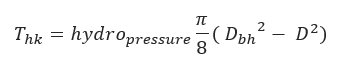
T_hk = hydro kinetic force (lbs)
D_bh = Borehole diameter, usually 1.5.D (inch)

Straight section A-B

Friction from Soil:

𝑓𝑟𝑖𝑐₂ = 𝑊_𝑆𝐿₁𝑐𝑜𝑠𝜃𝑆₁𝜇_{𝑆𝑜𝑖𝑙}

L1 – Length of the straight section 1
θS1 – Angle in degrees from horizontal for straight section 1
μSoil – Average coefficient of friction between pipe and soil. Recommended value between .21-.3 (Maidla)

Drag Forces from Mud:

𝐷𝑟𝑎𝑔₂ = 𝜋𝐷𝐿₁𝜇_𝑚𝑢𝑑

μmud – Fluid drag coefficient for steel tube pulled through bentonite mud

Tension on Section:

∆𝑇₂ = |𝑓𝑟𝑖𝑐₂| + 𝐷𝑟𝑎𝑔₂ − 𝑊_𝑠𝐿₁𝑠𝑖𝑛𝜃_𝑠1 + 𝑇_ℎ𝑘

Cumulative Pull Load:

𝑇₂ = ∆𝑇₂ + 𝑇₁

T₁ – Pull back as the pipe enters the drill hole (lbf)

Curved Section B-C

(based on Roark’s solution for elastic beam deflection)
θ_C1 – Angle in degrees from horizontal for curved section 1
R1- Radius of curvature of curve section 1 (ft)
L_arc1 – Length of curved section 1(ft)
E – Young’s Modulus (psi)

Friction from Soil:

𝑓𝑟𝑖𝑐 = |𝑁3𝜇𝑆𝑜𝑖𝑙|

Drag Forces from Mud:

𝐷𝑟𝑎𝑔₃ = 𝜋𝐷𝐿_{𝑎𝑟𝑐1}𝜇_𝑚𝑢𝑑

Tension on Section:

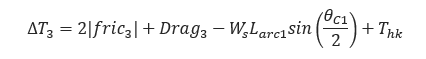
Cumulative Pull Load:

𝑇₃ = ∆𝑇₃ + 𝑇₂

Straight Section C-D

Friction from Soil:

𝑓𝑟𝑖𝑐₄ = 𝑊_𝑆𝐿_𝑠𝑐𝑜𝑠𝜃_𝑆𝜇_{𝑆𝑜𝑖𝑙}

Ls – Length of straight section between bends (ft)
θs – – Angle in degrees from horizontal for straight sections between bends

Drag Forces from Mud:

𝐷𝑟𝑎𝑔₄ = 𝜋𝐷𝐿_𝑠𝜇_𝑚𝑢𝑑

Tension on Section:

∆𝑇₄ = |𝑓𝑟𝑖𝑐₄| +𝐷𝑟𝑎𝑔₄ – 𝑊_𝑠𝐿_𝑠𝑠𝑖𝑛𝜃_𝑠 + 𝑇_ℎ𝑘

Cumulative Pull Load:

𝑇₄ = ∆𝑇₄ + 𝑇₃

Curved Section D-E

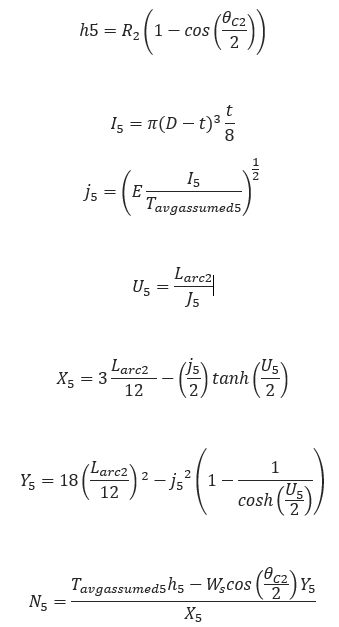
θ_C2 – Angle in degrees from horizontal for curved section 2
R₂– Radius of curvature of curve section 2 (ft)
L_arc2 – Length of curved section 2(ft)

Friction from Soil:

𝑓𝑟𝑖𝑐 = |𝑁₅𝜇_{𝑆𝑜𝑖𝑙}|

Drag Forces from Mud:

𝐷𝑟𝑎𝑔₅ = 𝜋𝐷𝐿_{𝑎𝑟𝑐2}𝜇_𝑚𝑢𝑑

Tension on Section:

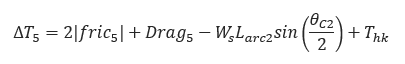
Cumulative Pull Load:

𝑇₅ = ∆𝑇₅ + 𝑇₄

Straight Section E-F

Friction from Soil:

𝑓𝑟𝑖𝑐₆ = 𝑊_𝑆𝐿₂𝑐𝑜𝑠𝜃_𝑆2𝜇_{𝑆𝑜𝑖𝑙}

Drag Forces from Mud:

𝐷𝑟𝑎𝑔₆ = 𝜋𝐷𝐿₂𝜇_𝑚𝑢𝑑

Tension on Section:

∆𝑇₆ = |𝑓𝑟𝑖𝑐₆| + 𝐷𝑟𝑎𝑔₆ – 𝑊_𝑠𝐿₁𝑠𝑖𝑛𝜃_𝑠12 – Length of the straight section 2

θ_S2 – Angle in degrees from horizontal for straight section 2

Cumulative Pull Load:

𝑇₆ = ∆𝑇₆ + 𝑇₅

Total pull load of the pipe:

𝑇_{𝑡𝑜𝑡𝑎𝑙} = ∆𝑇₂ + ∆𝑇₃ + ∆𝑇₄ + ∆𝑇₅ + ∆𝑇₆

T_total – Total pull load of the pipe (lbf)

Bending Strain:

R = 40 D

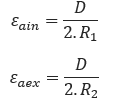
Bending Stress:

𝛿_𝑎𝑖𝑛 = 𝐸24.𝜀_𝑎𝑖𝑛

𝛿_𝑎𝑒𝑥 = 𝐸24.𝜀_𝑎𝑒𝑥

E₂₄ = 24 hr-Apparent Modulus of Elasticity (psi)

Allowable Tensile Stress:

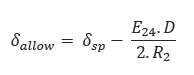
δ_sp – Allowable/Safe Pull Stress (psi)

Tensile Stress at Point A:

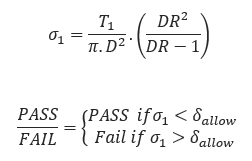
Tensile Stress at Point B:

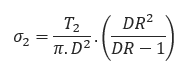
Tensile Stress at Point C:

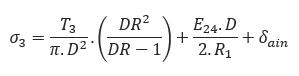
Tensile Stress at Point D:

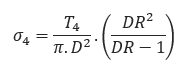
Tensile Stress at Point E:

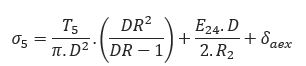
Tensile Stress at Point F:

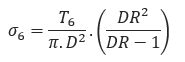
Breakaway Links Settings:

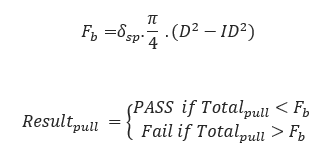
Static Head Pressure:

𝑃_𝑒𝑥𝑡 = 𝜌_𝑤•𝛾_𝑏•𝐻

H = depth of the bore profile (ft), usually the depth of the horizontal section

Maximum Pressure During Pull back

𝑃𝑚𝑎𝑥 = 𝑃𝑒𝑥𝑡 + ℎ𝑦𝑑𝑟𝑜𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒

Ovality Compensation Factor:

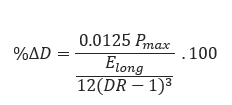
Buoyant Deformation:

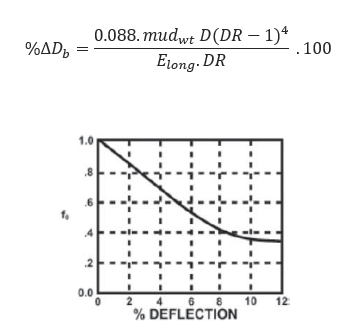
f₀ – Ovality compensation factor based on % of Deflection

Tensile Reduction Factor:

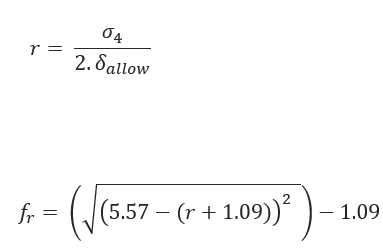
Critical Collapse Pressure:

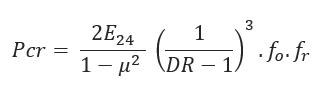
Safety Factor:

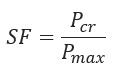
Input Parameters

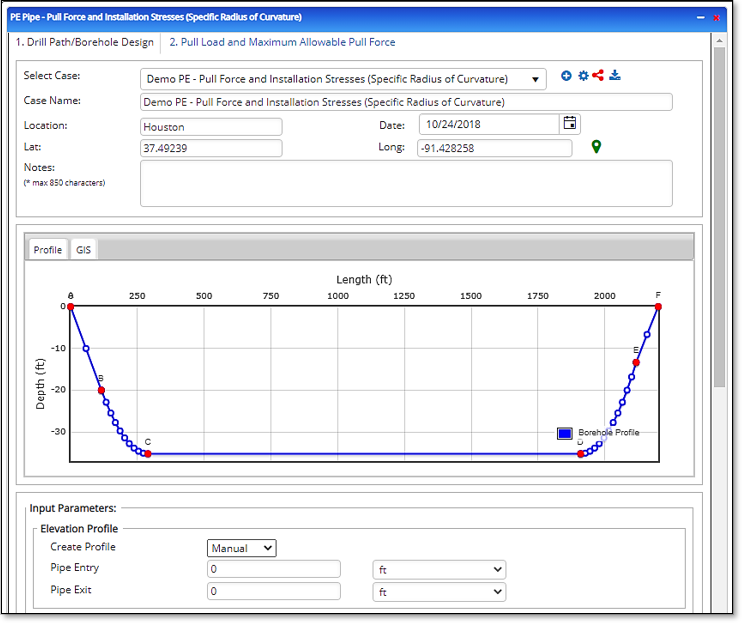
Elevation Profile:

Create Profile
Pipe Entry
Pipe Exit

Drill Path/Borehole Design: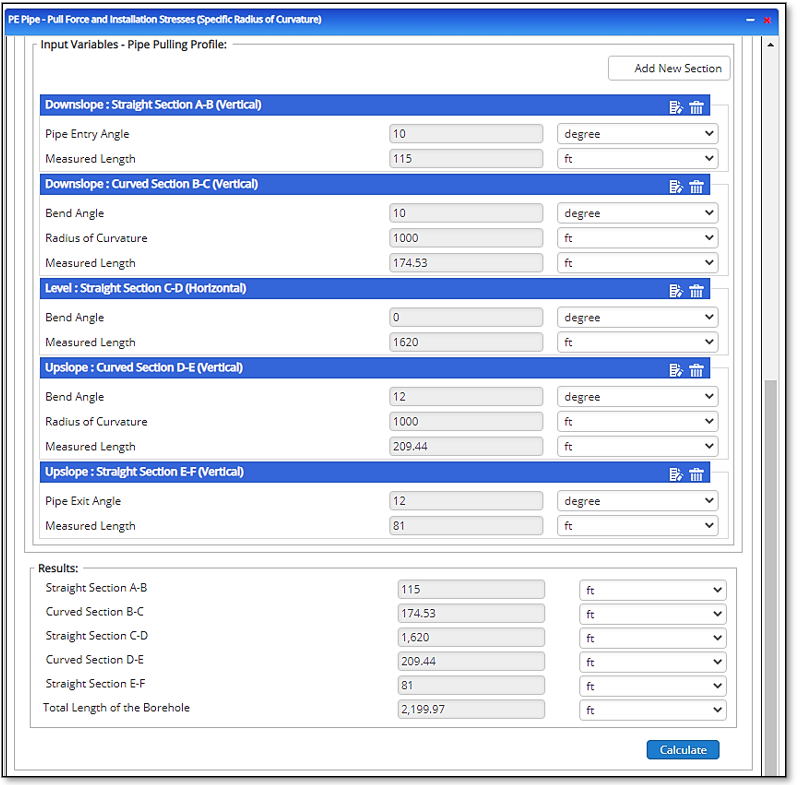

Downslope: Straight Section A – B (Vertical)
- Pipe Entry Angle A – B [degree]
- Measured Length [ft]
Downslope:
Curved Section B – C (Vertical)
- Bend Angle B – C [degree]
- Radius of Curvature B – C [ft]
- Measured Length [ft]
Straight Section C – D (Horizontal)
- Horizontal Angle[degree]
- Measured Length [ft]
Upslope: Curved Section D – E (Vertical)
- Radius of Curvature D – E
- Measured Length [ft]
Upslope: Straight Section E – F (Vertical)
- Pipe Exit Angle[degree]
- Measured Length [ft]

*The design changes based on borehole design (section configuration)

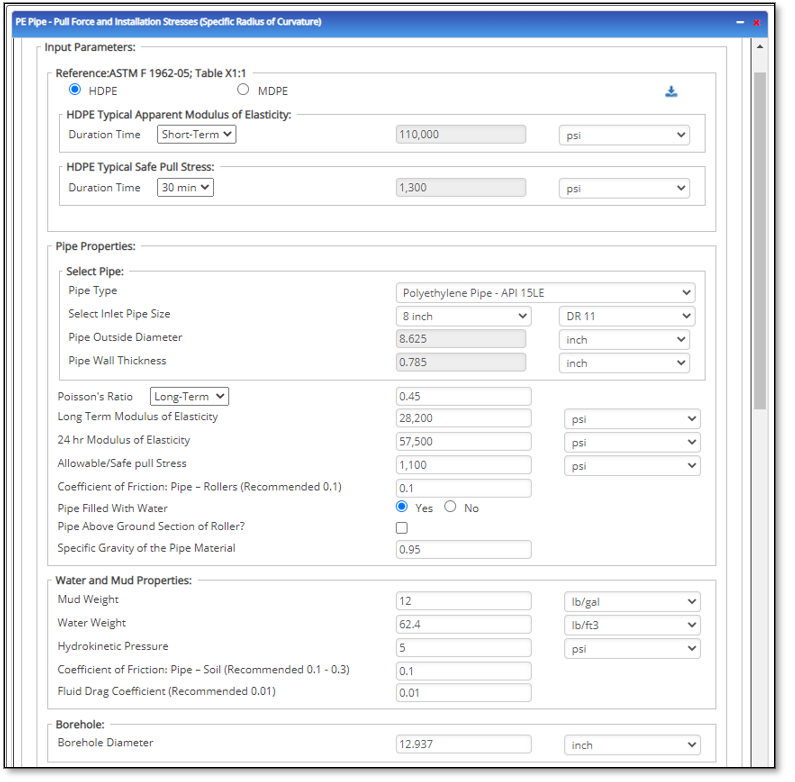
Pipe Properties:

Pipe Type
Select Inlet Pipe Size (in)
- Pipe Outside Diameter (in)
- Pipe Wall Thickness(in)
Standard Dimension Ratio (DR)
Long Term Modulus of Elasticity (psi)
Poisson’s Ratio
24 hr. Modulus of Elasticity
Allowable Safe Pull Stress (psi)
Coefficient of Friction: Pipe – Rollers (0.1)
Pipe Filled with Water (Y/N
Pipe Above Ground Section of Roller (Check Box)
- Angle of pipe Above Ground on Roller (°)
- Pipe Section Above Ground on Roller (ft.)
Specific Gravity of Pipe Material

Water and Mud Properties:

Mud Weight (lbs./gal)
Water Weight(lbs./ft3)
Hydrokinetic Pressure
Coefficient of Friction: Pipe – Soil (0.1 – 3)
Fluid Drag Coefficient (Recommended (0.01)

Borehole:

Borehole Diameter (in)

Outputs/Reports

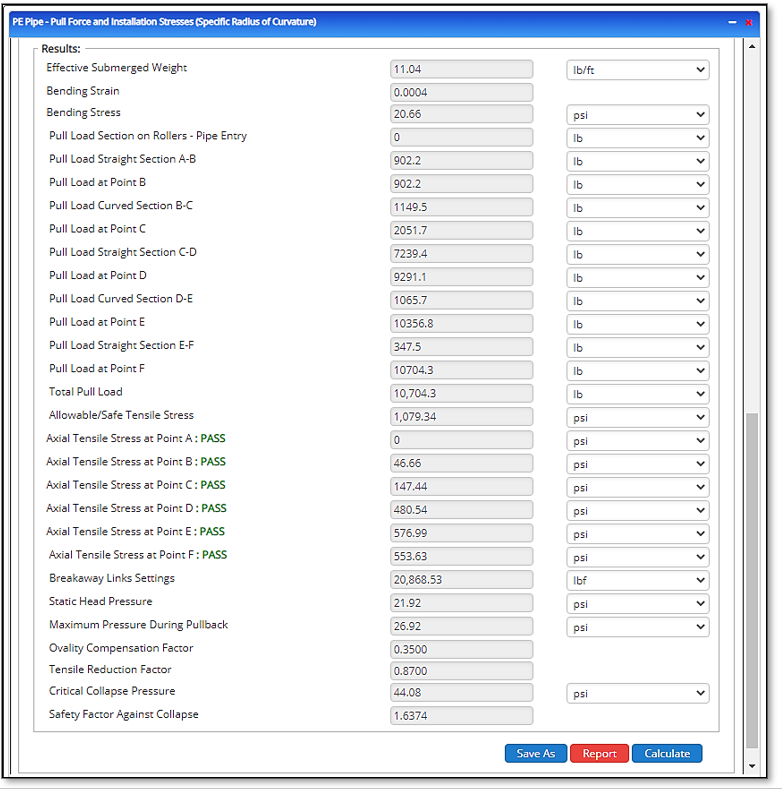
Results:

Effective Submerged Weight
Bending Strain
Bending Stress
Pull Load Section on Rollers – Pipe Entry
Pull Load Straight Section A-B
Pull Load at Point B
Pull Load Curved Section B-C
Pull Load at Point C
Pull Load Straight Section C-D
Pull Load at Point D
Pull Load Curved Section D-E
Pull Load at Point E
Pull Load Straight Section E-F
Pull Load at Point F
Total Pull Load
Allowable/Safe Tensile Stress
Axial Tensile Stress at Point A: PASS
Axial Tensile Stress at Point B: PASS
Axial Tensile Stress at Point C: PASS
Axial Tensile Stress at Point D: PASS
Axial Tensile Stress at Point E: PASS
Tensile Stress at Point F: PASS
Breakaway Links Settings
Static Head Pressure
Maximum Pressure During Pullback
Ovality Compensation Factor
Tensile Reduction Factor
Critical Collapse Pressure
Safety Factor Against Collapse