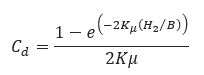Track Load Analysis

Introduction

The Track Load Program was designed to calculate the overburden and track loads on buried pipe with a Single Layer System (soil only). The information used to design this program was taken from the Newmark’s Integration of the Boussinesq Equation which considered the theoretical work done by M.G. Spangler on overburden and vehicle loads on buried pipe. This analysis does not evaluate cyclic loading, but the API 1102 calculation does.

Variables and Boundary Conditions 

REQUIRED INFORMATION:
1. Values for all the following variables:

𝐻₂ −Cover, Vertical Depth from the Ground to the Top of the Pipe (ft.)

𝐵 − Trench Width (ft.)

𝐷_𝑠 − Weight per unit Volume of Backfill (lbs/ft³)

𝐷 − Outside Diameter of the Pipe (in.)

𝑆𝑀𝑌𝑆 − Specified Minimum Yield Stress of the Pipe (psi.)

𝑃 − Pipe Internal Pressure (psi.)

𝑇 − Pipe Wall Thickness (in.)

2. Variables for the following information about the track:

𝐿_𝑡 − Operating Weight of the Object Crossing the Pipeline with Tracks(lbs)

𝑇_𝑤 − Width of the Standard Track Shoe(in)

𝑇_𝑙 − Length of the Track on the Ground(ft)

𝑇_𝑔 − Track Gauge(ft)

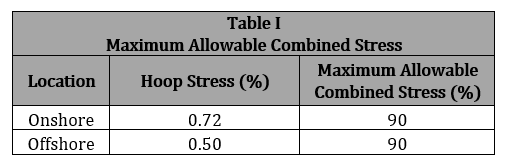
3. The Design Factor of the pipeline being analyzed is used to find the Maximum Allowable Combined Stress (% SMYS), (0.72 is the standard factor used for liquid).

4. The Soil Type which is used to find the friction force coefficients (Km), see Table II.

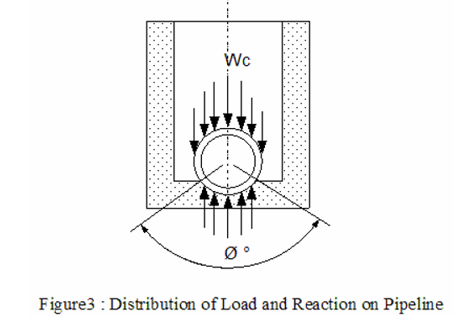
5. The Crossing Construction Type which is used to find the bedding constants for buried pipe (Kb & Kz), see Table V & Figure 3.

6. All the above information along with values for the following variables:

X – Longitudinal Distance over which Deflection Occurs (ft.)
Y – Vertical Deflection (in.)

Workflow

As a first estimate of the soil load on the pipe it could be assumed that the backfill soil slides down the trench walls without friction. Additionally, assume that all soil above the pipe is supported by the pipe itself and that the backfill soil on either side of the pipe does not assist in this support.

These assumptions are very conservative, but they help a great deal in initial understanding of the method of solution. The assumptions yield a soil load on the pipe equal to the weight of the backfill soil above the pipe. This analysis provides an estimate of soil loads on the buried pipe if nothing else is known about the system.

The basic analysis developed by M.G. Spangler follows similar arguments to that given above. In this analysis, Spangler includes frictional forces between the trench wall and the backfill. This permits the weight of the overburden to be partially carried by the surrounding soil and reduces the total soil load on the pipe. The resulting equations for calculating the pipe load due to overburden are as follows:

𝐶_𝑑 − Trench Coefficient

𝐵 − Trench Width(ft)

𝐻₂ − Cover, vertical depth from the ground surface to top of pipe(ft)

𝐾_𝜇 − Coefficient of friction force between the backfill soil and the trench wall.

Cd determines how much load is carried by the pipe. If there is no soil friction Cd becomes equal to H/B and the entire backfill load must be supported by the pipeline. The term Kμ provides a coefficient of friction force between the backfill soil and the trench wall. A high value of Kμ implies that friction between the backfill and trench wall is high and the weight of the backfill is supported largely by the wall friction. A low value implies that there is little friction encountered and the backfill is allowed to settle more such that the weight must be supported by the pipe. Table II provides values of Kμ used in the program for five different soil types. Also, in Table II are examples of values for Ds, the
density which is the weight per unit of backfill, which may be used if an actual value is not known. Note: If a value for Ds is already given use that value instead of the one in Table II.

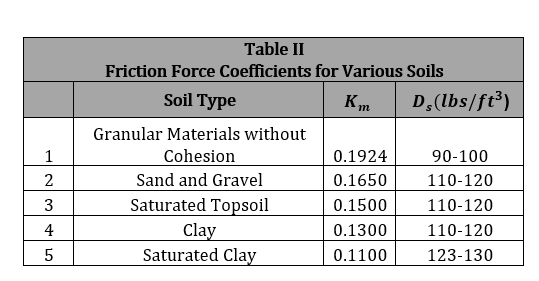
The soil types and coefficients given in this table represent the range that could normally be expected. Saturated clay has little internal friction so that it has the smallest value for Kμ. This implies that almost all of the soil load is carried by the pipe. Granular materials have a great deal more internal friction. Their value of Kμ is higher which leads us to the conclusion that the pipe carries less of the backfill load. Spangler, in his work, recommends using the value for clay in most instances. Higher values may be used when there is adequate evidence that the internal friction is higher and warrants a higher value of Kμ.
Spangler’s recommendation provides a conservative estimate for common buried pipe situations. Marsh and bog areas, however, have friction properties more similar to saturated clay such that a value for Km equal to 0.110 should be used in these areas.

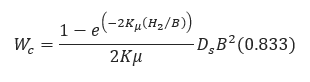
𝑊_𝑐 − Load per unit Length of the Pipe due to Overburden(lbs/in)

𝐵 − Trench Width(ft)

𝐻₂ − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)

𝐷_𝑠 − Density which is the Weight per unit of Backfill(lbs/ft³)

𝐾_𝜇 − Coefficient of Friction Force between the Backfill Soil and the Trench Wall.

The Impact Factor (I) for a track load calculation with a single layer system is always going to be 1.5. The reason for this is that the impact factor for soil is 1.5 and that is the only thing that separates the track from the pipe in a single layer system.

Calculating track load is somewhat different from calculating a wheel load because the load of a track expands over a larger area rather than a single point as does the wheel load. The information needed from the track are the operating weight (Lt) of the object crossing the pipeline with tracks is measured in lbs., the width of the standard track shoe (Tw) measured in inches, the length of the track on the ground (Tl) measured in ft., and the track gauge (Tg) measured in ft.

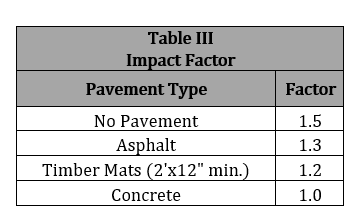
The weight of a track can be considered as a uniformly distributed load applied at the top of the soil over an area equal to the length of the track on the ground times the width of the standard track shoe. On the basis of this assumption, the unit pressure at a point on the top of the line pipe or casing pipe directly beneath the center of the area may be estimated by means on Newmarks Integration of Boussinesq equation. Newmark determined the pressure at a point in the undersoil at any elevation below one corner of the rectangular area over which unit loads are uniformly applied, and gave influence coefficients corresponding to the Influence Factor m and Influence Factor n.

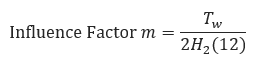
𝐻₂ − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)

𝑇_𝑤 − width of the standard track shoe(in)

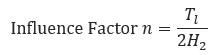
𝐻₂ − Cover, Vertical Depth from the Ground Surface to Top of Pipe(ft)

𝑇_𝑙 − Length of the track on the ground(ft)

These two factors are used by M.G. Spangler in the table called “Influence Coefficients for Solution of Holl’s and Newmark’s Integration of the Boussinesq Equation for Vertical Stress”, see Table VI. Both of the influence factors will be rounded off to the nearest 0.01 in order to cross reference Table VI.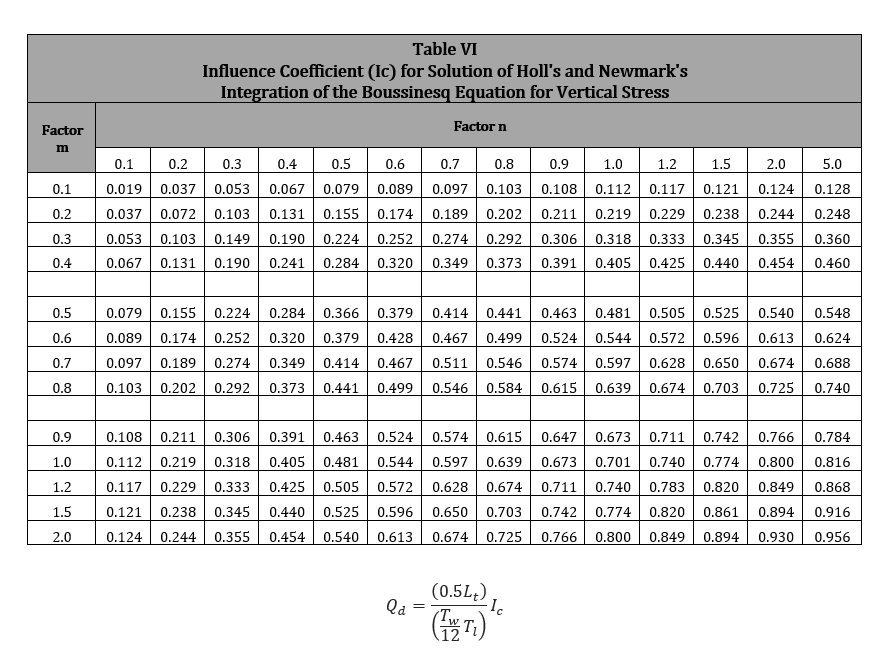

𝑄_𝑑 − Maximum static pressure on the pipe directly under the center of the object with tracks(lbs/ft²)

𝐼_𝑐 − Influence Coefficient selected from Table IV

𝐿_𝑡 − Operating weight of the object crossing the pipeline with tracks(lbs)

𝑇_𝑤 − Width of standard track show(in)

The equation for Qd is widely employed in structural work to estimate the unit pressure on a deep soil stratum below a foundation, it appears to be appropriate for this problem. The constant equal to 0.5 will be multiplied by Lt to get the operating load of one track.

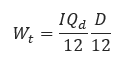
𝑊_𝑡 − Total track load on the pipe(lbs/in)

𝐷 − Outside diameter of the pipe(in)

𝐼 − Impact factor

𝑄_𝑑 − Maximum static pressure on the pipe directly under the center of the object with tracks(lbs/ft²)

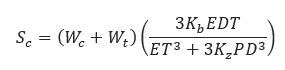
𝑆_𝑐 − Circumferential stress due to pipe wall deflection(psi)

𝐷 − Outside Diameter of the pipe(in)

𝐸 − Pipe material modulus of elasticity (2.9 x 10⁷)

𝐾_𝑏 − Bending coefficient which is a function of the crossing construction types

𝐾_𝑧 − Deflection coefficient which is a function of the crossing construction types

𝑃 − Pipe internal pressure (psi)

𝑇 − Pipe wall thickness(in)

𝑊_𝑐 − Load per unit length of pipe due to overburden(lbs/in)

𝑊_𝑡 − Total track load on pipe(lbs/in)

Note that the equation Sc includes pressure in the denominator so that bending stresses are reduced by increasing pressure.
Equation Sc, as well as equation St, have two constants which depend upon the bedding material upon which the pipe is placed. This bedding material is based on the crossing construction type. When the pipe is placed on a rigid bedding such as an Open Cut-Rock, little soil deformation occurs so that the load application area on the bottom is very small.
However, if the pipe is placed on soil, the support conforms to the pipe somewhat and the load is distributed over a larger area (See Figure 3). The latter case produces less pipe stress and is preferable. Spangler’s formulation includes both of these possibilities in order to provide a conservative estimate for the rigid bedding case without penalizing the soil bedding case. It does so by varying the constants Kb and Kz. Spangler’s recommended values for the constants are provided in Table V.

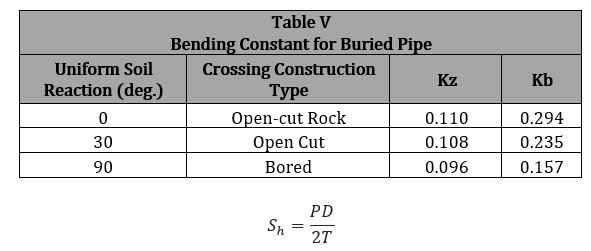
𝑆_ℎ − Hoop Stress due to Internal Pressure(psi)

𝐷 − Outside Diameter of the Pipe(in)

𝑃 − Pipe Internal Pressure(psi)

𝑇 − Pipe Wall Thickness(in)

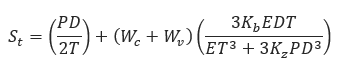
St is the total circumferential stress in the pipe wall due to pressure (hoop) stress and bending stresses resulting from circumferential flexure caused by external loads measured in PSI. The first term on the right-hand side of the equation is the formula for hoop stress due to internal pressure (Sh) and the second term is the formula for circumferential stress due to pipe wall deflection (Sc). Longitudinal Bending Stress (Sb) is when the overburden and vehicle load on buried pipelines will cause pipe settlement into the soil in the bottom of the trench. This settlement occurs because soil is not as stiff as the pipe and will deform easily as the pipe is “pushed” downward. Under uniform soil conditions and overburden loading, the pipe will settle evenly into the trench bottom along its entire length. Soil is not generally uniform, however, and regions of “softer” soil will occur adjacent to regions of stiff soil, so that the pipe will settle unevenly and hence bending will occur. A load that is applied on only one portion of a pipeline will cause the section of pipe under the load to settle more than the unloaded pipe, such that bending will also result. Longitudinal bending stress occurs in tension on the outside of the bend and in compression on the inside of the bend. Tensile stress is represented with a positive value for Sb; conversely, compressive stress takes a negative value for Sb. The longitudinal bending stress is calculated as follows:

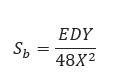
𝑆_𝑏 − Longitudinal Bending Stress(psi)

𝐷 − Outside Diameter of the Pipe(in)

𝐸 − Pipe Material Modulus of Elasticity(2.9 x 10⁷)

𝑋 − Longitudinal Distance over which Deflection occurs(ft)

𝑌 − Vertical Deflection(in)

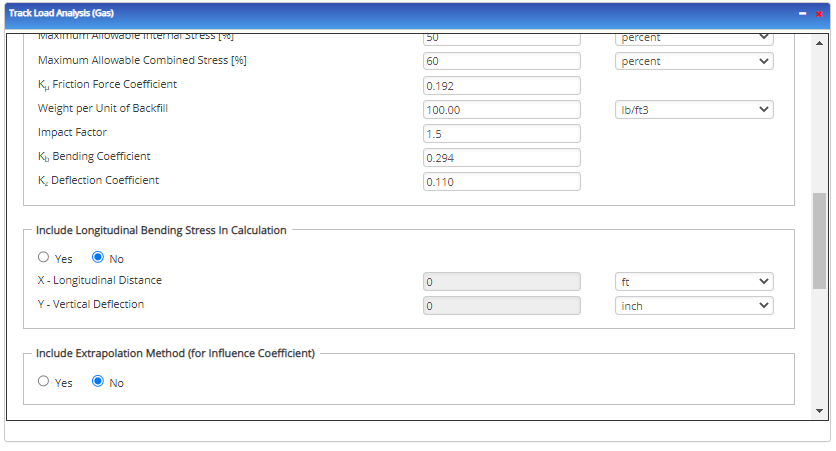
A negative value will be used when calculating the total combined stress (S). This will result in a larger (more conservative) combined stress. Note: If longitudinal bending stress does occur, click onto the designated box next to “Longitudinal Bending Stress”. If the box is not marked, then the program will assume “0” for Sb.

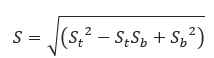
𝑆 − Total Combined Stress by Von Mises(psi)

𝑆_𝑏 − Longitudinal Bending Stress(psi)

𝑆_𝑡 − Total Circumferential Flexure caused by External Loads(psi)

Note that if longitudinal bending stress is not present then the S will equal St. The final calculation is % SMYS. This is calculated to determine if the current conditions exceed the Maximum Allowable Combined Stress determined by Transcontinental Gas Pipe Line Corporation.

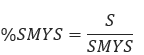
S – Total Combined Stress by Von Mises(psi)
SMYS – Specified Minimum Yield Strength(psi)

Input Parameters

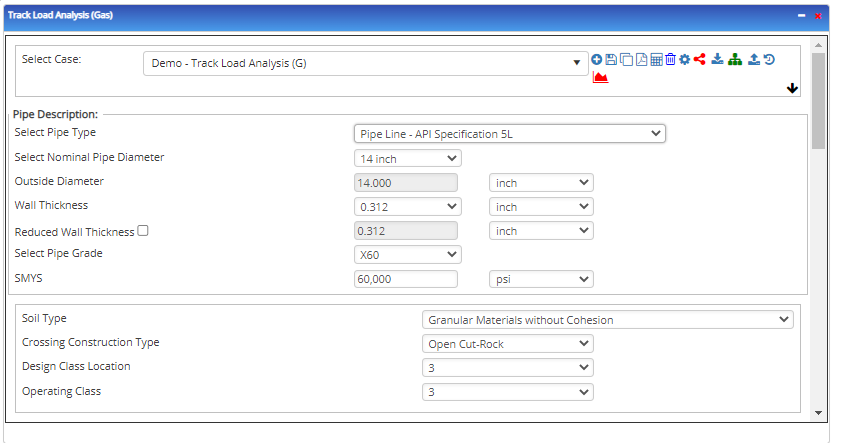
1. To create a new case, click the “Add Case” button
2. Select the Track Load Analysis application from the Pipeline Crossing module.
3. Enter Case Name, Location, Date and any necessary notes.
4. Fill out all required fields.
5. Make sure the values you are inputting are in the correct units.
6. Click the CALCULATE button.

• Nominal Pipe Size(in):(1/8” – 48”)
• Pipe Outside Diameter(in):(0.625” – 48”)
• Pipe Wall Thickness(in):(0.068”- >2”)
• Design Location
• Operation Class
• Soil Type
• Crossing Construction Type
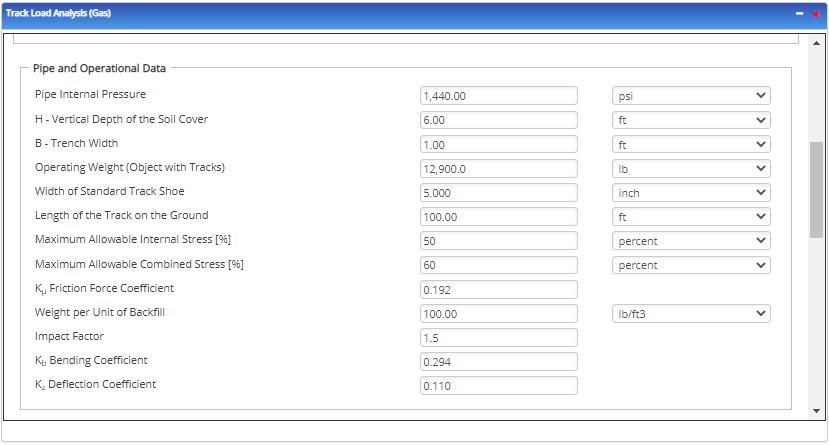
• Maximum Allowable Internal Stress
• Maximum Allowable Combined Stress
• Friction Force Coefficient
• Weight Per Unit of Backfill
• Impact Factor
• Bending Coefficient
• Deflection Coefficient
• Pipe Internal Pressure
• Operating Weight
• Vertical Depth of the Soil Cover
• Width of Standard Track Shoe
• Trench Width
• Specified Minimum Yield Stress:(24000psi-80000psi)
• Length of the Track on Ground
• Include Longitudinal Bending Stress in Calculation
• X – Longitudinal Distance
• Y – Vertical Deflection
• Include Extrapolation Method (for Influence Coefficient)

Outputs/Reports

1. View the results.
2. If an input parameter needs to be edited be sure to hit the CALCULATE button after the change.
3. To SAVE, fill out all required case details then click the SAVE button.
4. To rename an existing file, click the SAVE As button. Provide all case info then click SAVE.
5. To generate a REPORT, click the REPORT button.
6. The user may export the Case/Report by clicking the Export to Excel/PowerPoint icon.
7. To delete a case, click the DELETE icon near the top of the widget.

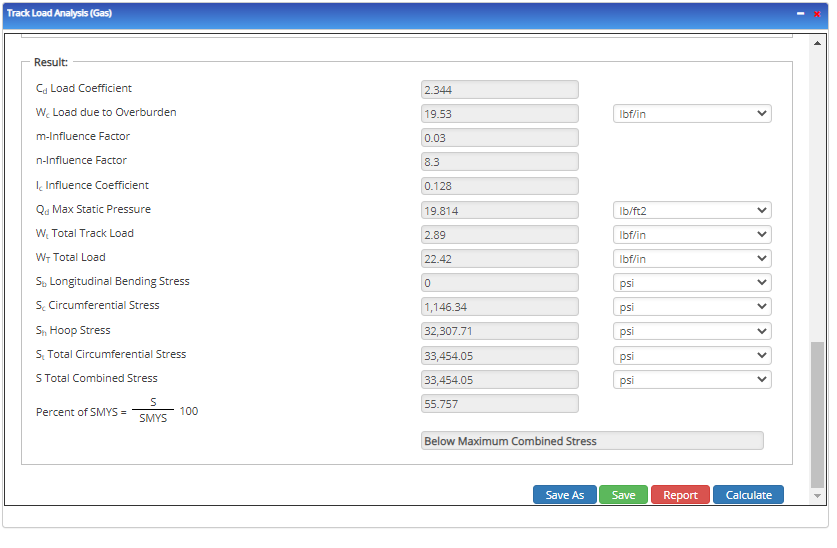
• Load Coefficient
• Load due to Overburden
• m – Influence Factor
• n – Influence Factor
• Influence Coefficient
• Maximum Static Pressure
• Total Track Load
• Total Load
• Longitudinal Bending Stress
• Circumferential Stress
• Hoop Stress
• Total Circumferential Stress
• Total Combined Stress
• Percent Of SMYS
• Status

Related Links